Fique com as Questões de Sólidos no ENEM separadas por assunto. Em cada questão temos a resposta comentada. Abaixo temos as questões do ENEM sobre Sólidos.
Questão 1
Q1791F (ENEM) Uma empresa produz e vende um tipo de chocolate, maciço, em formato de cone circular reto com as medidas do diâmetro da base e da altura iguais a 8 cm e 10 cm, respectivamente, como apresenta a figura.
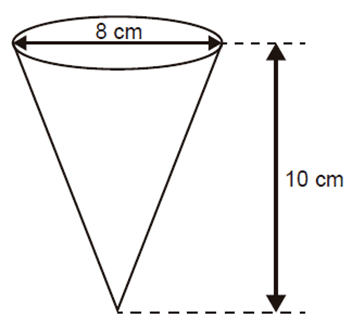
Devido a um aumento de preço dos ingredientes utilizados na produção desse chocolate, a empresa decide produzir esse mesmo tipo de chocolate com um volume 19% menor, no mesmo formato de cone circular reto com altura de 10 cm.
Para isso, a empresa produzirá esses novos chocolates com medida do raio da base, em centímetro, igual a
a) 1,52.
b) 3,24.
c) 3,60.
d) 6,48.
e) 7,20.
Resposta
Sendo o volume 19% menor, temos 81% do volume original, daí:
$\frac{81}{100} \cdot V= \frac{81}{100} \cdot \frac{1}{3} \cdot π \cdot 4^{2} \cdot 10=$
$\frac{9^{2}}{10^{2}} \cdot \frac{1}{3} \cdot π \cdot 4^{2} \cdot 10=$
$(\frac{9 \cdot 4 }{10})^{2} \cdot \frac{1}{3} \cdot π \cdot 10=$
$(3,6)^{2} \cdot \frac{1}{3} \cdot π \cdot 10=$
Então, o raio será 3,6
Letra C
Questão 2
Q1883F (ENEM) Um casal planeja construir em sua chácara uma piscina com o formato de um paralelepípedo reto retângulo com capacidade para 90 000 L de água. O casal contratou uma empresa de construções que apresentou cinco projetos com diferentes combinações nas dimensões internas de profundidade, largura e comprimento. A piscina a ser construída terá revestimento interno em suas paredes e fundo com uma mesma cerâmica, e o casal irá escolher o projeto que exija a menor área de revestimento.
As dimensões internas de profundidade, largura e comprimento, respectivamente, para cada um dos projetos, são:
• projeto I: 1,8 m, 2,0 m e 25,0 m;
• projeto II: 2,0 m, 5,0 m e 9,0 m;
• projeto III: 1,0 m, 6,0 m e 15,0 m;
• projeto IV: 1,5 m, 15,0 m e 4,0 m;
• projeto V: 2,5 m, 3,0 m e 12,0 m.
O projeto que o casal deverá escolher será o
a) I.
b) II.
c) III.
d) IV.
e) V.
Resposta
Resolvida em vídeo:
Sejam P, L e C respectivamente a profundidade, a largura e o comprimento da piscina.
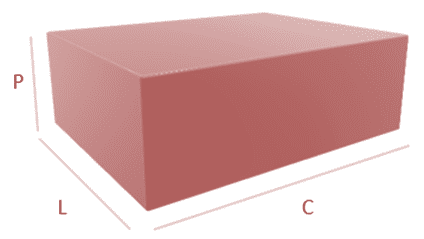
Para revestir a área interna da piscina, precisamos revestir as duas paredes laterais, o piso e as paredes frontais e traseiras. Ou seja, a área a ser revestida em cada projeto pode ser definida da seguinte forma:
$A=\underbrace{C \cdot L}_\text{Piso} + \underbrace{2 \cdot P \cdot L}_\text{Paredes Lat.} + \underbrace{2 \cdot C \cdot P}_\text{Paredes T. e F.}$
Dessa forma, as áreas a serem revestidas em cada projeto são:
Projeto I = 147,2 m²
Projeto II = 101 m²
Projeto III = 132 m²
Projeto IV = 117m²
Projeto V = 111 m²
Ou seja, o projeto que exige a menor área de revestimento é o projeto II.
Letra B
Questão 3
Q1885F (ENEM) Peças metálicas de aeronaves abandonadas em aeroportos serão recicladas. Uma dessas peças é maciça e tem o formato cilíndrico, com a medida do raio da base igual a 4 cm e a da altura igual a 50 cm. Ela será derretida, e o volume de metal resultante será utilizado para a fabricação de esferas maciças com diâmetro de 1 cm, a serem usadas para confeccionar rolamentos. Para estimar a quantidade de esferas que poderão ser produzidas a partir de cada uma das peças cilíndricas, admite-se que não ocorre perda de material durante o processo de derretimento.
Quantas dessas esferas poderão ser obtidas a partir de cada peça cilíndrica?
A) 800
B) 1 200
C) 2 400
D) 4 800
E) 6 400
Resposta
Resolvida em vídeo:
O volume de uma peça em formato cilíndrico:
$V=A_{b} \cdot h$
$=4^{2} \cdot π \cdot 5$
$=80π$
O volume de uma peça em formato esférico com raio $\frac{1}{2}$ :
Faremos a divisão para sabermos quantas esferas podemos obter de 80π
$80π \div \frac{\pi}{6}=80π \cdot \frac{6}{\pi}=4800$
Letra D
Questão 4
Q752M (ENEM) Dentre as diversas planificações possíveis para o cubo, uma delas é a que se encontra apresentada na Figura 1.
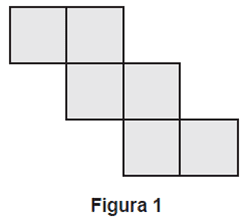
Em um cubo, foram pintados, em três de suas faces, quadrados de cor cinza escura, que ocupam um quarto dessas faces, tendo esses três quadrados um vértice em comum, conforme ilustrado na Figura 2.
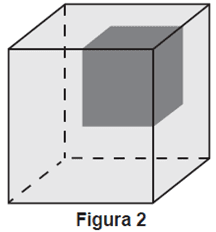
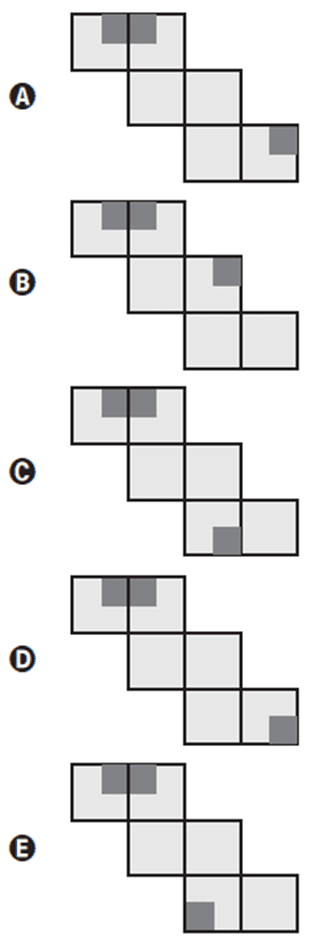
Resposta
Observe a figura a seguir, em que V é o vértice comum às faces A, B e F.
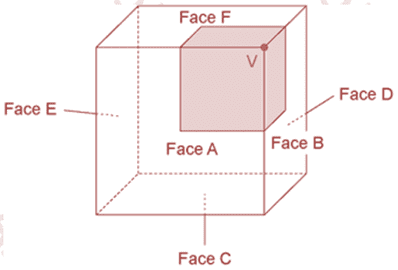
Dessa forma, a planificação esperada é:
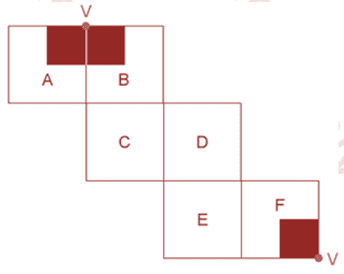
Letra D
Questão 5
Q1904F (ENEM) Uma loja comercializa cinco modelos de caixas-d’água (I, II, III, IV e V), todos em formato de cilindro reto de base circular. Os modelos II, III, IV e V têm as especificações de suas dimensões dadas em relação às dimensões do modelo I, cuja profundidade é P e área da base é Ab, como segue:
- modelo II: o dobro da profundidade e a metade da área da base do modelo I;
- modelo III: o dobro da profundidade e a metade do raio da base do modelo I;
- modelo IV: a metade da profundidade e o dobro da área da base do modelo I;
- modelo V: a metade da profundidade e o dobro do raio da base do modelo I.
Uma pessoa pretende comprar nessa loja o modelo de caixa-d’água que ofereça a maior capacidade volumétrica. O modelo escolhido deve ser o
A) I.
B) II.
C) III.
D) IV.
E) V.
Resposta
Em formato cilíndrico, temos o modelo I com volume $V=A_{b} \cdot h$ , para nosso caso, a altura h será a profundidade P ou seja, $V=Ar^{2} \cdot h$
modelo II: o dobro da profundidade e a metade da área da base do modelo I;
$V_{II}=\frac{\pi r^{2}}{2} \cdot 2P$
$V_{II}=Ar^{2} \cdot h$
$V_{II}=V_{I}$
modelo III: o dobro da profundidade e a metade do raio da base do modelo I;
$V_{III}=\pi \cdot \left( \frac{r}{2} \right) ^{2} \cdot 2P$
$V_{III}=\frac{ \pi \cdot r^{2}}{2} \cdot P$
$V_{II}=\frac{V_{I}}{2}$
modelo IV: a metade da profundidade e o dobro da área da base do modelo I;
$V_{IV}=2\pi r^{2} \cdot\frac{h}{2}$
$V_{IV}=\pi \cdot r^{2} \cdot h$
$V_{IV}=V_{I}$
modelo V: a metade da profundidade e o dobro do raio da base do modelo I.
$V_{V}=\pi (2r)^{2} \cdot \frac{h}{2}$
$V_{V}=\pi (4r)^{2} \cdot h$
$V_{V}=4 \cdot V_{I}$
Portanto, o modelo V oferece a maior capacidade volumétrica.
Letra E
Questão 6
Q1913F (ENEM) Uma cozinheira produz docinhos especiais por encomenda. Usando uma receita-base de massa, ela prepara uma porção, com a qual produz 50 docinhos maciços de formato esférico, com 2 cm de diâmetro. Um cliente encomenda 150 desses docinhos, mas pede que cada um tenha formato esférico com 4 cm de diâmetro. A cozinheira pretende preparar o número exato de porções da receita-base de massa necessário para produzir os docinhos dessa encomenda.
Quantas porções da receita-base de massa ela deve preparar para atender esse cliente?
A) 2
B) 3
C) 6
D) 12
E) 24
Resposta
Ao calcular a razão entre o volume de massa da porção de doces encomendados e o volume de massa da porção de doces da receita-base, temos:
$\frac{150 \cdot \frac{4}{3}\cdot \pi \cdot 2^{3}}{50 \cdot \frac{4}{3}\cdot \pi \cdot 1^{3}}=24$
Letra E