Fique com as questões de função no ENEM. Em cada questão temos a resposta comentada.
Questão 1
Q1909F (ENEM) Em uma competição de velocidade, diz-se que há uma ultrapassagem quando um veículo que está atrás de outro passa à sua frente, com ambos se deslocando no mesmo sentido. Considere uma competição automobilística entre cinco carros em uma pista com 100 m de comprimento, onde todos largam no mesmo instante e da mesma linha. O gráfico mostra a variação da distância percorrida por cada veículo, em função do tempo, durante toda a competição.

Qual o número de ultrapassagens, após o início da competição, efetuadas pelo veículo que chegou em último lugar?
A) 0
B) 1
C) 2
D) 3
E) 4
Resposta
Observando o gráfico, o veículo que chegou em último é representado pelo segmento de menor inclinação. Logo, verifica-se que esse veículo não efetuou ultrapassagem, só foi ultrapassado.
Letra A
Questão 2
Q1793F (ENEM) O funcionário de uma loja tem seu salário mensal formado por uma parcela fixa de 675 reais mais uma comissão que depende da quantidade de peças vendidas por ele no mês. O cálculo do valor dessa comissão é feito de acordo com estes critérios:
• Até a quinquagésima peça vendida, paga-se 5 reais por peça;
• A partir da quinquagésima primeira peça vendida, o valor pago é de 7 reais por peça.
Represente por q a quantidade de peças vendidas no mês por esse funcionário, e por S(q) o seu salário mensal, em real, nesse mês.
A expressão algébrica que descreve S(q) em função de q é
a) S(q) = 675 + 12q
b) S(q) = 325 + 12q
c) S(q) = 675 + 7q
D) $S(q)= \left\{ \begin{array}{cl} 625 + 5q, \text{se q}≤50 \\ 925 + 7q, \text{se q}>50 \end{array}\right.$
E) $S(q)= \left\{ \begin{array}{cl} 625 + 5q, \text{se q}≤50 \\ 575 + 7q, \text{se q}>50 \end{array}\right.$
Resposta
Resolvida em vídeo:
A primeira sentença é dada por:
S(q) = 675 + 5q
A segunda sentença é dada por:
S(q) = x + 7q
Em que x é um valor inicial desconhecido. Observando o esboço do gráfico abaixo, vemos que há um ponto em comum entre as duas funções (q = 50)
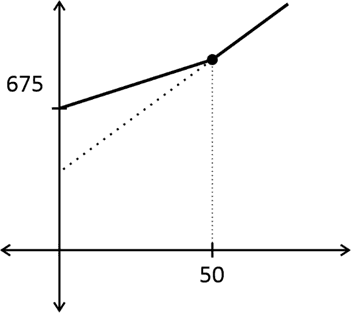
Portanto:
675 + 5q = x + 7q
675 + 5.50 = x + 7.50
575 = x
A resposta correta será:
$S(q)= \left\{ \begin{array}{cl} 675 + 5q, \text{se q}≤50 \\ 575 + 7q, \text{se q}>50 \end{array}\right.$
Anulada.
Questão 3:
Q734M (ENEM) Ao analisar os dados de uma epidemia em uma cidade, peritos obtiveram um modelo que avalia a quantidade de pessoas infectadas a cada mês, ao longo de um ano. O modelo é dado por p(t) = −t² + 10t + 24, sendo t um número natural, variando de 1 a 12, que representa os meses do ano, e p(t) a quantidade de pessoas infectadas no mês t do ano.
Para tentar diminuir o número de infectados no próximo ano, a Secretaria Municipal de Saúde decidiu intensificar a propaganda oficial sobre os cuidados com a epidemia. Foram apresentadas cinco propostas (I, II, III, IV e V), com diferentes períodos de intensificação das propagandas:
• I: 1 ≤ t ≤ 2;
• II: 3 ≤ t ≤ 4;
• III: 5 ≤ t ≤ 6;
• IV: 7 ≤ t ≤ 9;
• V: 10 ≤ t ≤ 12.
A sugestão dos peritos é que seja escolhida a proposta cujo período de intensificação da propaganda englobe o mês em que, segundo o modelo, há a maior quantidade de infectados. A sugestão foi aceita. A proposta escolhida foi a
a) I.
b) II.
c) III.
d) IV.
e) V.
Resposta
Resolvida em vídeo: clique aqui
Considerando a função p(t) = −t² + 10t + 24, calcularemos o Xv:
$X=\frac{-b}{2a}=\frac{-10}{2(-1)}=5$
Letra C
Questão 4
Q1888F (ENEM) Em jogos de voleibol, um saque é invalidado se a bola atingir o teto do ginásio onde ocorre o jogo. Um jogador de uma equipe tem um saque que atinge uma grande altura. Seu recorde foi quando a batida do saque se iniciou a uma altura de 1,5 m do piso da quadra, e a trajetória da bola foi descrita pela parábola $y=$, em que y representa a altura da bola em relação ao eixo x (das abscissas) que está localizado a 1,5 m do piso da quadra, como representado na figura. Suponha que em todas as partidas algum saque desse jogador atinja a mesma altura do seu recorde.

A equipe desse jogador participou de um torneio de voleibol no qual jogou cinco partidas, cada uma delas em um ginásio diferente. As alturas dos tetos desses ginásios, em relação aos pisos das quadras, são:
• ginásio I: 17 m;
• ginásio II: 18 m;
• ginásio III: 19 m;
• ginásio IV: 21 m;
• ginásio V: 40 m.
O saque desse atleta foi invalidado
a) apenas no ginásio I.
b) apenas nos ginásios I e II.
c) apenas nos ginásios I, II e III.
d) apenas nos ginásios I, II, III e IV.
e) em todos os ginásios.
Resposta
Como se quer achar a altura máxima que a bola atinge em sua trajetória, deve-se achar o y do vértice:
$Y_{v}=\frac{-Δ}{4a}$
$=\frac{-((\frac{-7}{3})^{2}-4 \cdot(\frac{-1}{6}) \cdot 12)}{4 \cdot (\frac{-1}{6})}$
$=\frac{-((\frac{49}{9})+8)}{-\frac{2}{3}}$
$=\frac{121}{9}/cdot \frac{3}{2}$
$=\frac{121}{9}≅20,16$
Pela figura, a bola parte a 1,5m de altura, a altura máxima será: 20,16 + 1,5 = 21,66
Dessa forma, o saque será inválido em todas as quadras cujas alturas sejam inferiores a 21,5 m. Portanto, o saque será inválido nas quadras I, II, III e IV.
Letra D
Questão 5
Q748M (ENEM) Uma máquina em operação tem sua temperatura T monitorada por meio de um registro gráfico, ao longo do tempo t. Essa máquina possui um pistão cuja velocidade V varia com a temperatura T da máquina, de acordo com a expressão V = T² − 4. Após a máquina funcionar durante o intervalo de tempo de 10 horas, o seu operador analisa o registro gráfico, apresentado na figura, para avaliar a necessidade de eventuais ajustes, sabendo que a máquina apresenta falhas de funcionamento quando a velocidade do pistão se anula.
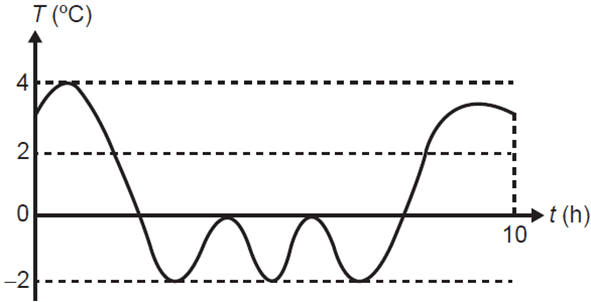
Quantas vezes a velocidade do pistão se anulou durante as 10 horas de funcionamento?
A) 1
B) 2
C) 3
D) 4
E) 5
Resposta
Resolvida em vídeo: https://youtu.be/wzTJNE2nROA
As falhas de funcionamento acontecem quando a velocidade V do pistão se anula.
A partir da equação V = T² – 4, temos:
V = T² – 4
0 = T² – 4
4 = T²
±2 = T
Analisando-se o gráfico, verifica-se que a temperatura T alcançou cinco vezes o valor 2 ou –2, nos pontos indicados na figura a seguir.
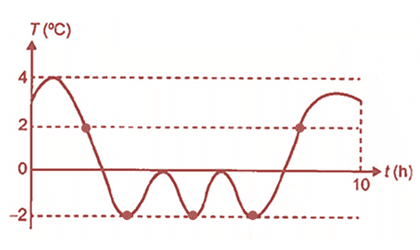
Letra E