[latexpage]
Fique com a prova resolvida da UEMA 2021. Em cada questão temos a resposta comentada.
Para mais conteúdo sobre a UEMA, clique aqui.
Questão 33 – 1° Dia
Q574M (UEMA) Em um debate entre candidatos à Prefeitura de uma determinada cidade, havia, no auditório, um público com um número de mulheres igual ao número de homens. Do total de presentes, sabe-se que 13,2% dos homens e 0,33% das mulheres apoiam o candidato A.
A probabilidade de que seja homem um apoiador do candidato A, selecionado ao acaso, é
a) 3/123
b) 1/2
c) 1287/100
d) 40/41
e) 1353/100
Resposta
Como temos ambos percentuais do mesmo inteiro, o total de apoiadores do candidato A será:
13,2 + 0,33 = 13,53
Fazendo a probabilidade para a escolha de um homem dentre os apoiadores de A:
$ \color{red} \frac{{13,2}}{{13,53}} = \frac{{13,20}}{{13,53}} = \frac{{{{1320}^{:3}}}}{{{{1353}^{:3}}}} = \frac{{{{440}^{:11}}}}{{{{451}^{:11}}}} = \frac{{40}}{{51}} $
Letra D
Resolução em vídeo: Clique Aqui
Questão 34 – 1° Dia
Q1351F (UEMA) Uma peça triangular, medindo 10m, 8m e 6m, feita de chapa uniforme, será içada por um guindaste por apenas um único ponto de contato, conforme a figura a seguir.
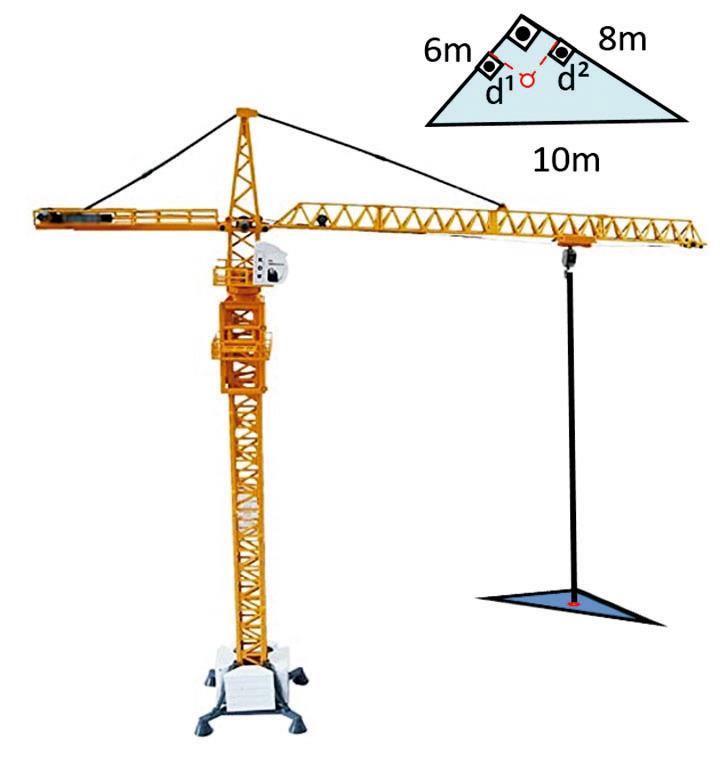
As distâncias d¹ e d², em metros, do ponto de içamento em relação aos menores lados desse triângulo para que a peça seja içada exatamente pelo ponto de encontro das três medianas são iguais a
a) 8/3 e 2
b) 5/3 e 2/3
c) 8/45 e 16/45
d) 10/3 e 3
e) 5 e 13/3
Resposta
Ilustrando a situação e traçando as medianas pedidas, teremos:
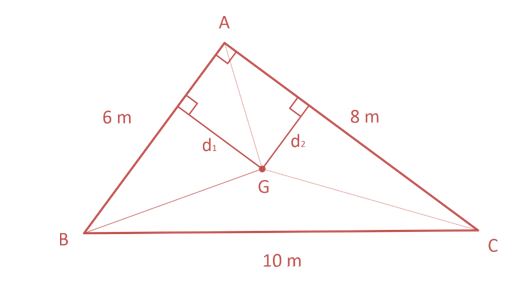
O triângulo ABC é possui área igual: $ \color{red} \frac{{6 \cdot 8}}{2} = 24 m$
O ponto G é o baricentro do triângulo ABC, logo os triângulos ABG, ACG e BCG possuem mesma área. Assim:
$ \color{red} {A_{ABG}} = \frac{{6 \cdot {d_1}}}{2} \Rightarrow \frac{{24}}{3} = \frac{{6 \cdot {d_1}}}{2} \Rightarrow 8 = 3 \cdot {d_1} \Rightarrow {d_1} = \frac{8}{3}$
$ \color{red} {A_{ACG}} = \frac{{8 \cdot {d_2}}}{2} \Rightarrow \frac{{24}}{3} = \frac{{8 \cdot {d_2}}}{2} \Rightarrow 8 = 4 \cdot {d_2} \Rightarrow {d_2} = 2$
Letra A
Resolução em vídeo: Clique Aqui
Questão 35 – 1° Dia
Q1352F (UEMA) Suponha que um carrinho de mão possui as dimensões de um tronco de pirâmide, conforme a figura a seguir.
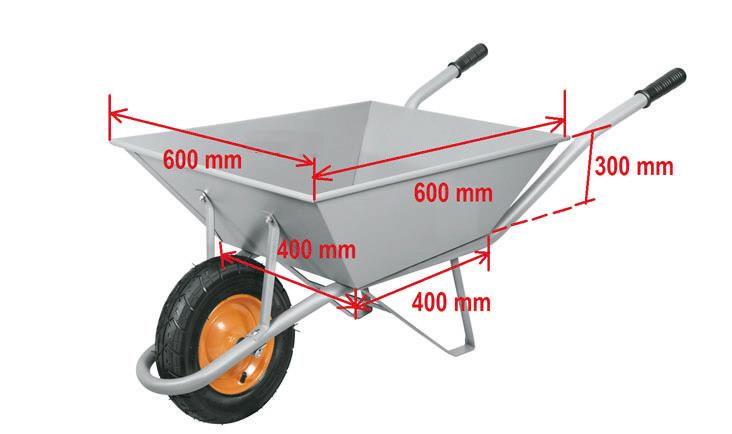
Quantos volumes desse carrinho de mão, completamente cheios de terra, serão necessários para transportar 1,90 m³ de areia?
a) 17
b) 40
c) 9
d) 25
e) 13
Resposta
Calculando a área da base maior e menor já em m³, teremos:
$ \color{red} {A_B} = {0,6^2} = 0,36\,{m^3} $
$ \color{red} {A_b} = {0,4^2} = 0,16\,{m^3}$
O volume do tronco de pirâmide é dado por:
$ \color{red} \begin{array}{c}
{V_T} = \frac{h}{3} \cdot \left( {{A_B} + \sqrt {{A_B} \cdot {A_b}} + {A_b}} \right) \Rightarrow \\
{V_T} = \frac{{0,3}}{3} \cdot \left( {0,36 + \sqrt {0,36 \cdot 0,16} + 0,16} \right) \Rightarrow \\
{V_T} = 0,1 \cdot \left( {0,52 + 0,6 \cdot 0,4} \right) \Rightarrow \\
{V_T} = 0,1 \cdot \left( {0,52 + 0,24} \right) \Rightarrow \\
{V_T} = 0,1 \cdot 0,76 = 0,076\,{m^3}
\end{array} $
Finalizando: $ \color{red} \frac{{1,9}}{{0,076}} = 25$
Letra D
Resolução em vídeo: Clique Aqui
Para mais conteúdo sobre a UEMA, clique aqui.
Questão 36 – 1° Dia
Q1353 (UEMA) A Catedral de Brasília tem formato circular, com centro no ponto Oe diâmetro de 70 m.
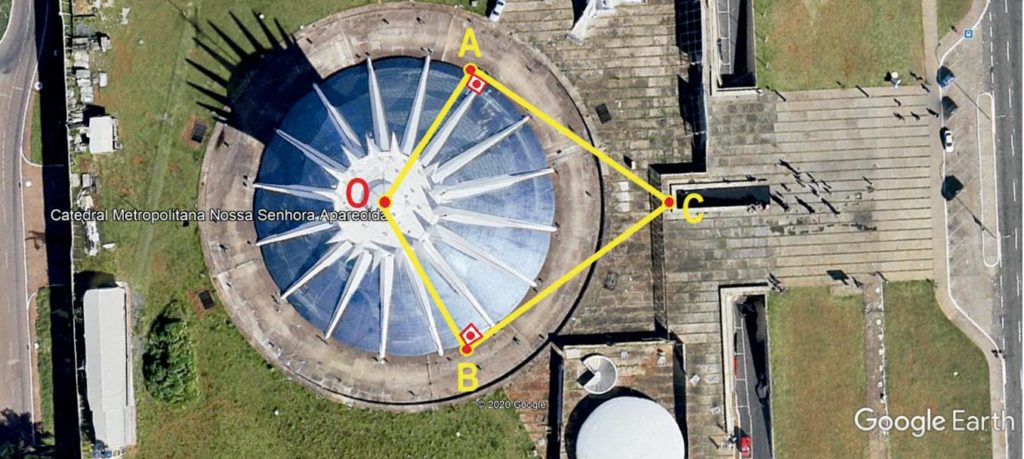
Um turista localizado no ponto C observa dois trabalhadores nos pontos A e B numa trajetória retilínea a x metros de distância de cada um. Sabendo que o arco AB é de 3 π/4 metros, nessas condições, o valor de x, em metros, é
a) $35 \cdot \sqrt {3 + 2\sqrt 2 } $
b) 35
c) $35 \cdot \sqrt {2 + 2\sqrt 2 } $
d) $35 \cdot \sqrt {3 – 2\sqrt 2 } $
e) $35 \cdot \sqrt {2 – 2\sqrt 2 } $
Resposta
Sendo o diâmetro 70 m, teremos o raio igual a 35 m. Na figura abaixo, destacaremos o ângulo central (igual ao arco)
$ \color{red} \frac{{3\pi }}{4} = \frac{{3 \cdot 180}}{4} = 3 \cdot 45 = 135^\circ $
Ilustrando e traçando o segmento AB, temos:
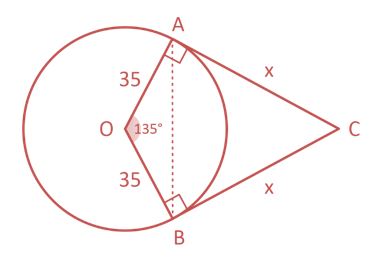
Agora, aplicaremos a lei dos cossenos em ABO:
$ \color{red} \begin{array}{c}
A{B^2} = {35^2} + {35^2} – 2 \cdot 35 \cdot 35 \cdot \cos 135^\circ \Rightarrow \\
A{B^2} = 2 \cdot {35^2} – 2 \cdot {35^2} \cdot \left( {\frac{{ – \sqrt 2 }}{2}} \right)\
A{B^2} = 2 \cdot {35^2} + 2 \cdot {35^2} \cdot \frac{{\sqrt 2 }}{2} \Rightarrow \\
A{B^2} = 2 \cdot {35^2} \cdot \left( {1 + \frac{{\sqrt 2 }}{2}} \right) \Rightarrow \\
A{B^2} = 2 \cdot {35^2} \cdot \frac{{2 + \sqrt 2 }}{2}\ A{B^2} = {35^2} \cdot \left( {2 + \sqrt 2 } \right) \Rightarrow \\
AB = 35 \cdot \sqrt {2 + \sqrt 2 }
\end{array}$
O ângulo C mede 45° e aplicando lei dos cossenos novamente:
$ \color{red} \begin{array}{c}
{\left( {35 \cdot \sqrt {2 + \sqrt 2 } } \right)^2} = {x^2} + {x^2} – 2 \cdot x \cdot x \cdot \cos 45 \Rightarrow \\
{\left( {35 \cdot \sqrt {2 + \sqrt 2 } } \right)^2} = 2{x^2} – 2{x^2} \cdot \frac{{\sqrt 2 }}{2} \Rightarrow \\
{\left( {35 \cdot \sqrt {2 + \sqrt 2 } } \right)^2} = 2{x^2} \cdot \left( {1 – \frac{{\sqrt 2 }}{2}} \right) \Rightarrow \\
{\left( {35 \cdot \sqrt {2 + \sqrt 2 } } \right)^2} = 2{x^2} \cdot \left( {\frac{{2 – \sqrt 2 }}{2}} \right) \Rightarrow \\
{\left( {35 \cdot \sqrt {2 + \sqrt 2 } } \right)^2} = {x^2} \cdot \left( {2 – \sqrt 2 } \right) \Rightarrow \\
{35^2} \cdot \left( {2 + \sqrt 2 } \right) = {x^2} \cdot \left( {2 – \sqrt 2 } \right) \Rightarrow \\
{x^2} = \frac{{{{35}^2} \cdot \left( {2 + \sqrt 2 } \right)\left( {2 + \sqrt 2 } \right)}}{{\left( {2 – \sqrt 2 } \right)\left( {2 + \sqrt 2 } \right)}} \Rightarrow
\end{array} $
desenvolvendo:
$ \color{red} \begin{array}{c}
{x^2} = \frac{{{{35}^2} \cdot \left( {2 + \sqrt 2 } \right)\left( {2 + \sqrt 2 } \right)}}{{\left( {2 – \sqrt 2 } \right)\left( {2 + \sqrt 2 } \right)}} \Rightarrow \\
{x^2} = \frac{{{{35}^2} \cdot \left( {4 + 4\sqrt 2 + 2} \right)}}{{4 – 2}} \Rightarrow \\
{x^2} = \frac{{{{35}^2} \cdot \left( {6 + 4\sqrt 2 } \right)}}{2} \Rightarrow \\
{x^2} = {35^2} \cdot \left( {3 + 2\sqrt 2 } \right) \Rightarrow \\
x = 35\sqrt {3 + 2\sqrt 2 }
\end{array} $
Letra A
Resolução em vídeo: Clique Aqui
Questão 33 – 2° Dia
Q576M (UEMA) Num comício com 1.800 apoiadores a uma candidatura a prefeito de uma cidade do interior brasileiro, foram identificadas todas as pessoas que estavam com COVID-19 e as gripadas. Ao final da identificação, constatou-s∈ Que 6% estavam com COVID-19; 3% estavam gripadas; 92% das pessoas não estavam com nenhuma das duas doenças.
Ao escolher um apoiador desse comício ao acaso e, sabendo que ele não está com COVID-19, qual a probabilidade d∈ Que esse apoiador esteja somente gripado?
a) 54/7
b) 3/91
c) 1/47
d) 5/188
d) 12/85
Resposta
Vemos que 6% + 3% + 92% = 101%, ou seja, há apoiadores sendo contados mais de uma vez em determinado grupo. Logo, vemos que há intersecção x entre os conjuntos:
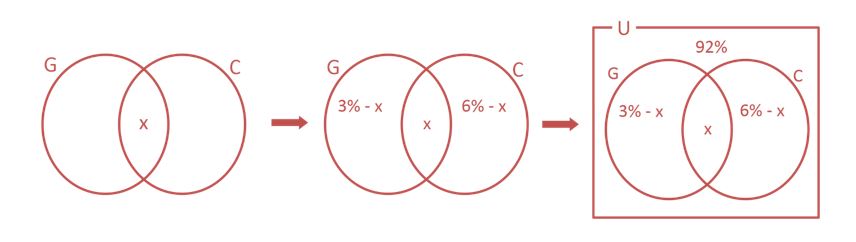
3% – x + x + 6% – x = 8% ⟹ 9% – x = 8% ⟹ x = 1%
Apoiadores com Covid: 6% – x + x = 6%
Somente Gripado: 3% – x = 3% – 1% = 2%
A escolha se dá dentre os que não estão com Covid (100% – 6% = 94%)
$ \color{red} P = \frac{{2\% }}{{94\% }} = \frac{1}{{47}}$
Letra C
Resolução em vídeo: Clique Aqui
Questão 34 – 2° Dia
Q577M (UEMA) Considere o triângulo retângulo ABC a seguir em que o comprimento do lado AB é o quádruplo do comprimento do lado BC e ainda que P seja o ponto médio de CB, K seja o ponto médio do segmento CP e F seja o ponto médio do segmento KP.
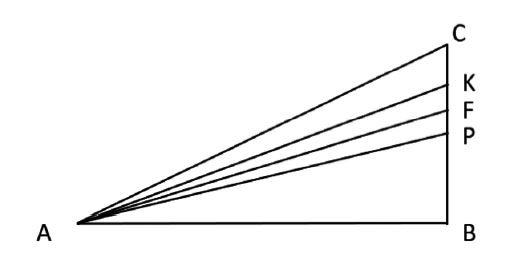
A tangente do ângulo FÂP é
a) 1/8
b) 8/261
c) 5/32
d) 3/16
e) 8/131
Resposta
Ilustrando a situação:
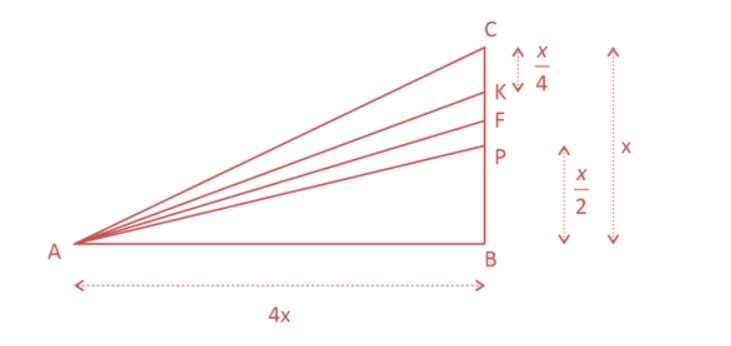
Ampliando a figura e destacando FÂP = θ:
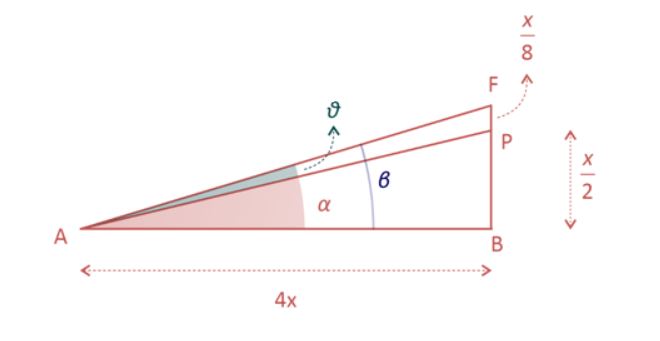
O segmento FB mede:
$ \color{red} \frac{x}{2} + \frac{x}{8} = \frac{{4x}}{8} + \frac{x}{8} = \frac{{5x}}{8}$
E note que β = α + θ ⟹ θ = β – α.
Lembrando que a tangente da diferença é
$ \color{red} tg\left( {\beta – \alpha } \right) = \frac{{tg\left( \beta \right) – tg\left( \alpha \right)}}{{1 + tg\left( \beta \right) \cdot tg\left( \alpha \right)}}$
Vamos calcular:
$ \color{red} tg\left( \alpha \right) = \frac{{\frac{x}{2}}}{{4x}} = \frac{x}{2} \cdot \frac{1}{{4x}} = \frac{1}{8}$
$ \color{red} tg\left( \beta \right) = \frac{{\frac{{5x}}{8}}}{{4x}} = \frac{{5x}}{8} \cdot \frac{1}{{4x}} = \frac{5}{{32}}$
Retomando tangente da diferença:
$ \color{red} tg\left( \theta \right) = tg\left( {\beta – \alpha } \right) = \frac{{\frac{5}{{32}} – \frac{1}{8}}}{{1 + \frac{5}{{32}} \cdot \frac{1}{8}}} = \\ \frac{{\frac{5}{{32}} – \frac{4}{{32}}}}{{1 + \frac{5}{{32 \cdot 8}}}} = \frac{{\frac{1}{{32}}}}{{\frac{{32 \cdot 8 + 5}}{{32 \cdot 8}}}} = \\ \frac{1}{{32}} \cdot \frac{{32 \cdot 8}}{{32 \cdot 8 + 5}} = \frac{8}{{261}} $
Letra B
Resolução em vídeo: Clique Aqui
Questão 35 – 2° Dia
Q578M (UEMA) O fabricante de uma das melhores bolas de basquete do país está colocando à venda uma embalagem cúbica, contendo 8 unidades, conforme a figura a seguir.
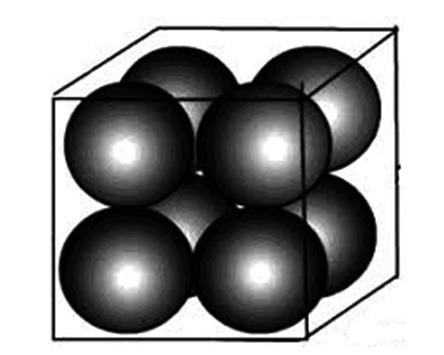
Considerando que cada bola de basquete tem raio igual a “r” cm e que tangenciam todos os lados internos das faces da embalagem cúbica, o valor, em cm³, do espaço vazio dentro da caixa, ou seja, o espaço não preenchido pelas bolas de basquete é
a) $latex \displaystyle \frac{{32{{r}^{3}}\left( {6-\pi } \right)}}{3}$
b) $latex \displaystyle \frac{{4{{r}^{3}}\left( {48-\pi } \right)}}{3}$
c) $latex \displaystyle \frac{{8{{r}^{3}}\left( {3-4\pi } \right)}}{3}$
d) $latex \displaystyle \frac{{4{{r}^{3}}\left( {6-\pi } \right)}}{3}$
e) $latex \displaystyle \frac{{32{{r}^{3}}\left( {3-\pi } \right)}}{3}$
Resposta
Sendo o raio da esfera r, a aresta do cubo vale 4r. O espaço vazio será:
$ \color{red} {\left( {4r} \right)^3} – 8 \cdot \frac{4}{3} \cdot \pi {r^3} = 64{r^3} – \frac{{32}}{3} \cdot \pi {r^3} = \\ \frac{{192{r^3} – 32\pi {r^3}}}{3} = \frac{{32{r^3}\left( {6 – \pi } \right)}}{3} $
Letra A
Resolução em vídeo: Clique Aqui
Questão 36 – 2° Dia
Q579M (UEMA) Numa concessionária de caminhões zero, o vendedor informou ao comprador que a lei matemática que permite estimar a depreciação do veículo comprado é
$v\left( t \right) = 65000 \cdot {4^{ – 0,04t}}$,
em que v(t) é o valor, em reais, do caminhão, t anos após a aquisição como zero na concessionária. Segundo a lei da depreciação indicada, o caminhão valerá um oitavo do valor de aquisição com
a) 37,5 anos.
b) 7,5 anos.
c) 25 anos.
d) 8 anos.
e) 27,5 anos.
Resposta
O valor inicial é 65 000, portanto:
$ \color{red} \begin{array}{c}
v\left( t \right) = 65000 \cdot {4^{ – 0,04t}} \Rightarrow \\
\frac{{65000}}{8} = 65000 \cdot {4^{ – 0,04t}} \Rightarrow \\
\frac{1}{8} = {4^{ – 0,04t}} \Rightarrow {2^{ – 3}} = {2^{ – 0,08t}} = \\
\frac{3}{{0,08}} = t = 37,5
\end{array}$
Letra A
Resolução em vídeo: Clique Aqui
Para mais conteúdo sobre a UEMA, clique aqui.