[latexpage]
Fique com a prova resolvida da UEMA 2020. Em cada questão temos as respostas comentadas do PAES UEMA
Para mais conteúdo da UEMA, clique aqui.
Questão 46 – 1ª Etapa
Anagramas, no âmbito da matemática, estão relacionados com a análise combinatória e consistem na permutação (troca de posição das letras) de uma palavra, resultando outra formação com exatamente as mesmas letras, podendo ter significado presente no dicionário ou não. Para sabermos o total de anagramas que são possíveis de serem formados, usamos o conceito de fatorial.
Por exemplo a palavra ALEGRIA com 7 letras, o resultado é 7! (7x6x5x4x3x2x1 = 5040) e para obter os anagramas basta trocar as letras entre si.
A quantidade de anagramas formados com a palavra PEDRA e quatro exemplos adequados destes anagramas estão indicados na seguinte opção:
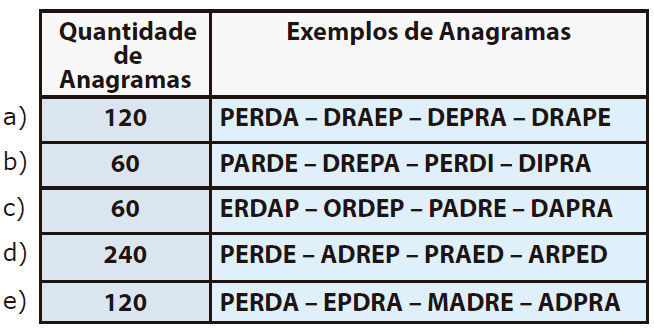
Resposta
Como a palavra PEDRA possui 5 letras diferentes, faremos:
P5 = 5! = 5.4.3.2.1 = 120
Note que na letra E temos um anagrama (MADRE) que não pertence ao conjunto de anagramas da palavra PEDRA.
Letra A
Questão 47 – 1ª Etapa
Os equipamentos elétricos vêm com um selo do INMETRO que indica o consumo de energia elétrica.
Analise a imagem do selo a seguir.

Nesse selo, afirma-se que o aparelho elétrico consome, em média, 57 kWh/mês (Quilowatt-hora por mês), ao funcionar 1 hora por dia. Um condicionador de ar funciona 4 horas por dia, todos os dias do mês, em um laboratório no Colégio Universitário em São Luís-MA. O valor pago, por kWh, é de RS 0,65. Ao final do mês, o custo, em reais, do consumo de energia desse aparelho será igual a
a) RS 228,00
b) RS 456,00
c) RS 339,00
d) RS 148,20
e) RS 84,00
Resposta
Sendo o consumo do ar condicionado no mês funcionando 1 hora por dia igual a 57 kWh e alterando para 4 horas por dia, em um mês, teremos: 4.57 = 228 kWh
O preço, então: 228.0,65 = RS 148,20
Letra D
Questão 48 – 1ª Etapa
A rede de satélites destinados para função GPS é de aproximadamente 30 satélites que circulam a Terra em seis diferentes órbitas pré-estabelecidas e distribuídas de uma maneira que, a qualquer momento e em qualquer ponto da terra, estão visíveis aos satélites. A área circular de cobertura de cada satélite cobre um conjunto de cidades. Em matemática, trabalhamos as operações de intersecção, de união, de diferença de conjuntos entre outras. Analise a imagem a seguir, considerando que os círculos são conjuntos e as cidades indicadas são elementos.
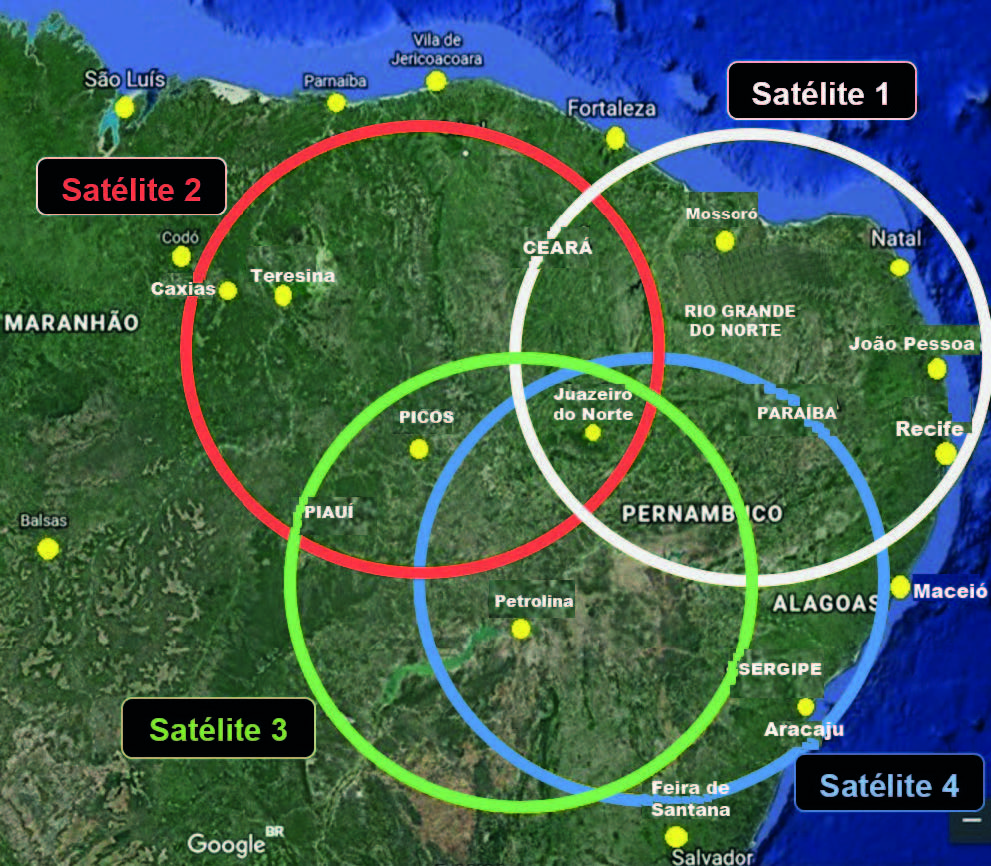
Em relação à imagem, é correto afirmar que
a) a intersecção das coberturas dos satélites 2, 3 e 4 compreende as cidades de Picos, Juazeiro do Norte e Petrolina.
b) a diferença entre os conjuntos das coberturas dos satélites 1 e 4 compreende as cidades de Petrolina, Aracaju e Juazeiro do Norte.
c) a união das coberturas dos satélites 3 e 4 compreende as cidades de Picos, Juazeiro do Norte, Petrolina, Aracaju e Salvador.
d) a diferença entre os conjuntos das coberturas dos satélites 2 e 3 compreende as cidades de Caxias, Teresina, Picos e Juazeiro do Norte.
e) a união das coberturas dos satélites 1, 2 e 3 compreende as cidades de Caxias, Picos, João Pessoa, Juazeiro do Norte, Natal, Petrolina, Recife, Teresina e Mossoró.
Resposta
Análise da Letra A:
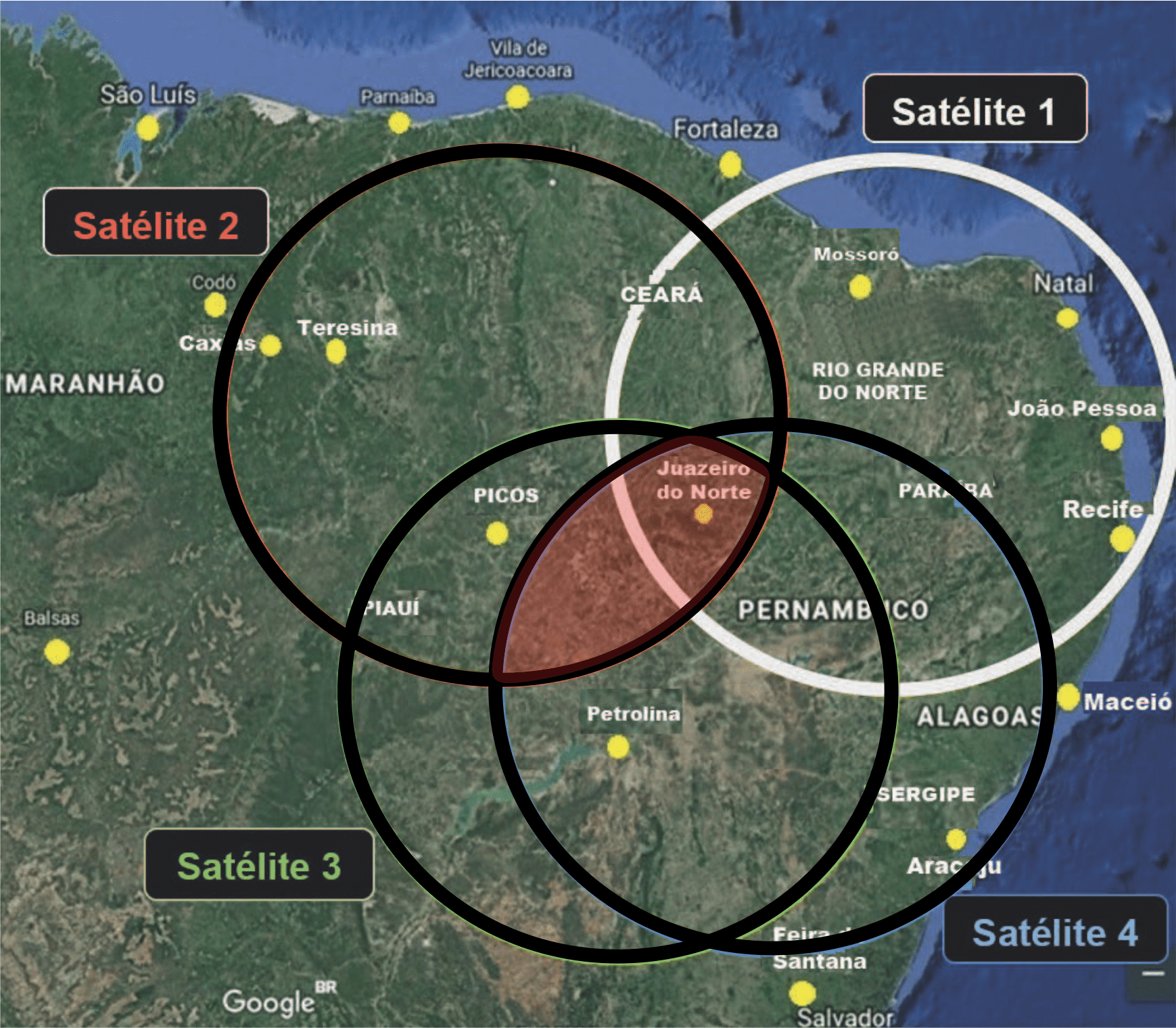
Pela imagem, vemos que na intersecção entre 2, 3 e 4 há somente a cidade de Juazeiro. (FALSA)
Análise da Letra B
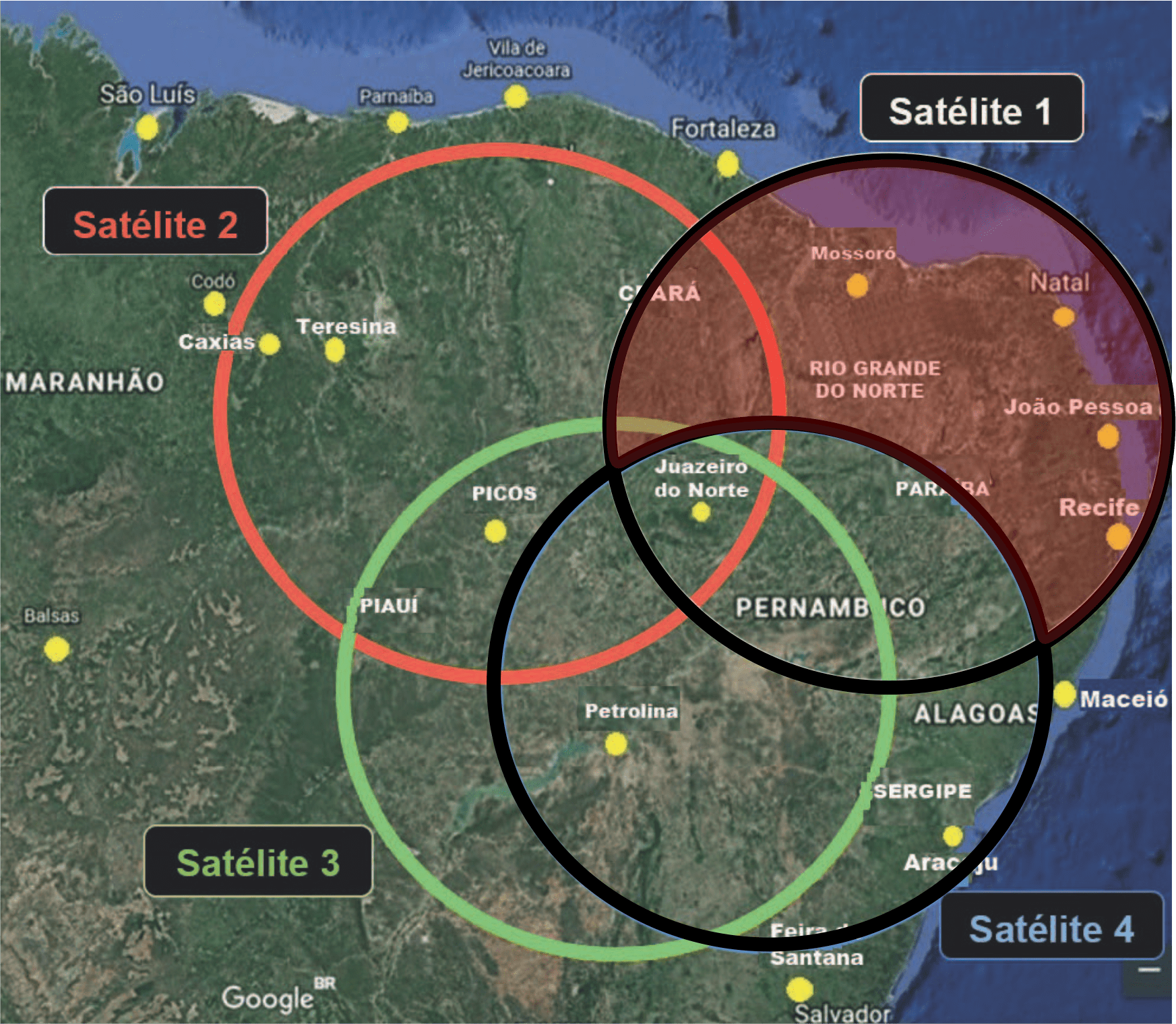
Pela imagem, vemos que Juazeiro não faz parte da diferença entre 1 e 4. (FALSA)
Análise da Letra C
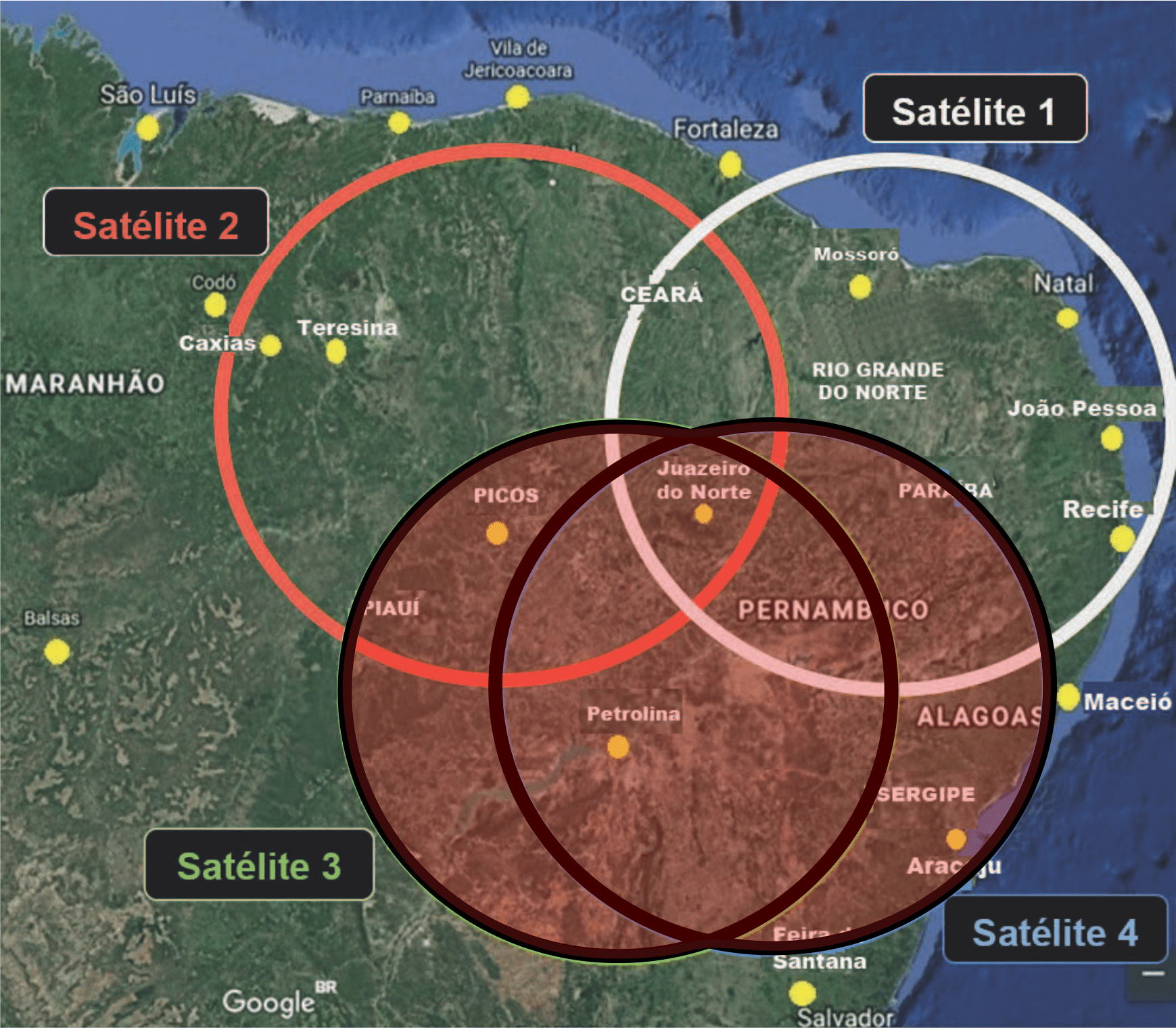
Pela imagem, vemos que Salvador não faz parte da união entre 3 e 4. (FALSA)
Análise da Letra D
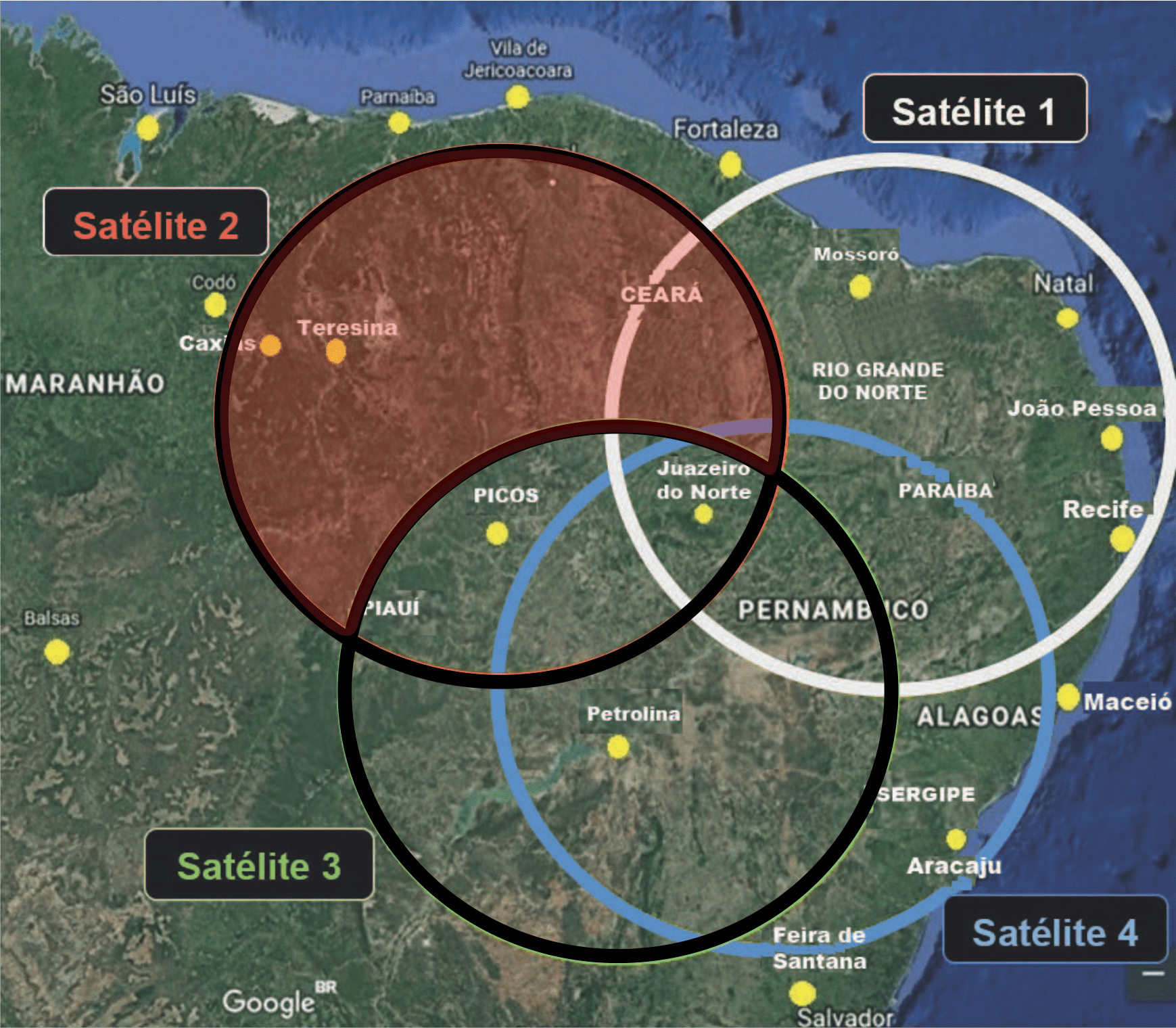
Pela imagem, vemos que Picos e Juazeiro não fazem parte da diferença entre 2 e 3. (FALSA)
Portanto, temos letra E como resposta da questão
Questão 49 – 1ª Etapa
O Complexo Deodoro, que engloba as praças Deodoro, Pantheon e as alamedas Gomes de Castro e Silva Maia, no Centro de São Luís, passou por uma grande reforma. Foram colocadas esferas como objeto de decoração, conforme imagem a seguir.

Em matemática, chamamos de esfera de centro O e raio R o conjunto de pontos do espaço cuja distância ao centro é menor ou igual ao raio R e ainda que seu volume é calculado como sendo quatro terços do valor de π multiplicado pelo cubo do raio da esfera. (use π=3,14).
O raio de uma das esferas é de, aproximadamente, 20cm e todas as esferas são iguais. O volume, em centímetros cúbicos, correspondente a 10 dessas esferas, é igual a, aproximadamente,
a) 33.933,34
b) 16.746,67
c) 334.933,33
d) 188.400,00
e) 18.840,00
Resposta
Para calcularmos o volume da esfera usaremos
$\color{red}\frac{4}{3} \cdot \pi {r^3}}$
Como são 10 esferas, teremos:
$ \color{red}10.\frac{4}{3}{{.3,14.20}^{3}}=\frac{{40.3,14.8000}}{3}\cong 334933,33 $
Letra C
Questão 50 – 1ª Etapa
O quadro ao lado representa o custo médio mensal de ração para cães em um hotel. Um casal adulto da raça Boxer e uma cadela adulta da raça Yorkshire ficarão dois meses no hotel para cães. O custo médio das rações consumidas pelos cães representa 34% da mensalidade a ser paga. O gasto total, em reais, por um período de dois meses, será de
a) RS 500,00
b) RS 800,00
c) RS 1.000,00
d) RS 971,42
e) RS 790,70

Resposta
Para um casal da raça Boxer, 2.78 = 156
Para uma cadela da raça Yorkshire 14.
Com ração, teremos o gasto de 156 + 14 = 170. Esse gasto representa 34% da mensalidade m:
$ \color{red}170= \frac{{34}}{{100}}m=\frac{{17000}}{{34}}=m=500 $
Letra A
Para mais conteúdo da UEMA, clique aqui.
Questão 01 – 2ª Etapa
Uma consultora de produtos de beleza precisa repor o seu estoque junto à distribuidora. Para tanto, gastou nas suas compras RS 345,00 para a reposição do estoque cujos preços, por unidade, são: RS 12,00, o batom e RS 7,00, o esmalte. Sabendo que foram adquiridas 35 unidades de produtos no total, calcule a quantidade de batons e de esmaltes comprados.
Resposta
Montaremos um sistema sendo b o número de batons e e o número de esmaltes
$latex \color{red}\left\{ \begin{array}{l}b+e=35\\12b+7e=345\end{array} \right.\Rightarrow \left{ \begin{array}{l}7b+7e=245\\12b+7e=345\end{array} \right.$
$latex \color{red}5b=100\Rightarrow b=20\therefore e=15$
Questão 02 – 2ª Etapa
O gráfico mostra os valores em bilhões de reais que o Brasil investiu em saneamento básico (2010 a 2017), de acordo com os dados da Confederação Nacional da Indústria. Mostra, ainda, os valores do gasto ideal, numa projeção por ano, para o período de 2018 a 2033, visando a acelerar os investimentos do setor para levar a coleta e o tratamento de esgoto a toda a população.
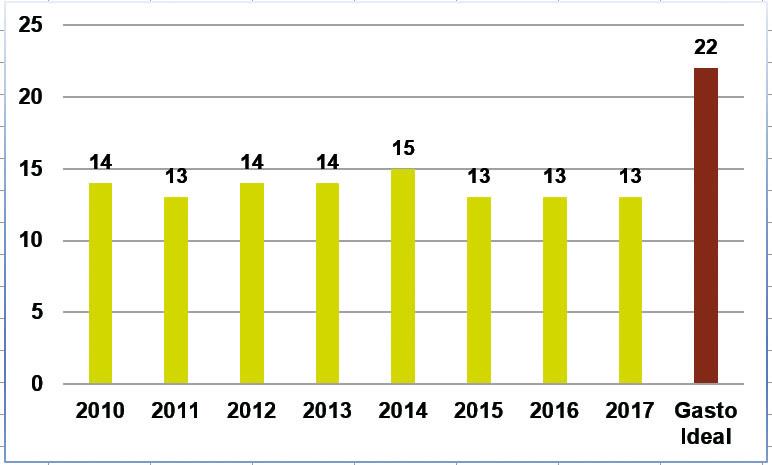
De um modo geral, tem sido amplamente divulgado pela mídia que, no ano de 2018, os investimentos foram aproximadamente 32% menores que os considerados como gasto ideal, de acordo com o gráfico. Calcule
a) o valor que teria sido necessário para atingir o gasto ideal nos investimentos, em 2018, no setor.
b) a média aritmética de investimento, em bilhões, referente aos anos de 2013 a 2016.
Resposta
a) Sendo o gasto ideal no valor de 22 bi e os investimentos em 2018 sendo 32% a menos, teremos:
$latex \color{red}\frac{{32}}{{100}}.22=\frac{{704}}{{100}}=7,04bi$
b) $latex \color{red}\frac{{14+15+13+13}}{4}=\frac{{55}}{4}=13,75bi$
Questão 03 – 2ª Etapa
A razão entre a massa de um material e o volume por ele ocupado é chamada de densidade. A unidade de medida da densidade, no Sistema Internacional de Unidades, é o quilograma por metro cúbico (kg/m³). Em determinadas condições, a água potável possui a densidade de 1.000kg/m³ e o Etanol (Álcool), sob as mesmas condições, possui densidade de 810kg/m³. Essa carreta bi trem, representada na imagem a seguir, quando em carga completa, tem capacidade para transportar 45.000 litros de produto por viagem.

O dono dessa carreta foi contratado para fazer três viagens com carga completa de etanol para um posto de combustível.
a) Calcule a massa, em kg, de produto Etanol, ao final das três viagens.
Resposta
a) Como a densidade é dada em m³, e 1m³ = 1000 litros, transformaremos: 45 000 L = 45m³
Usando a densidade do Etanol, após 3 viagens, teremos:
$latex \color{red}\frac{{810kg}}{{1{{m}^{3}}}}=\frac{x}{{3.45}}\Rightarrow x=810.135=109350kg$
Questão 04 – 2ª Etapa
O Porto do Itaqui, porto brasileiro localizado na cidade de São Luís do estado do Maranhão, é nacionalmente conhecido por ter uma das maiores amplitudes de maré do Brasil, podendo ultrapassar 7 metros. O Itaqui é o 11º no ranking geral e o 6º entre os portos públicos em movimentação de cargas. A profundidade de seu canal de acesso é de 23 metros. Frequentemente, existem navios atracando, descarregando, desatracando e à espera na baía de São Marcos. Analise a imagem a seguir.

Considere a medida do ângulo ACB=60°, a distância AC igual a 5 km e a distância CB igual a 8km. Nessas condições: (Use cos 60°=0,5), calcule a distância do navio A até o navio B, em km.
Resposta
Ilustrando a situação e usando a Lei dos Cossenos em triângulos quaisquer:
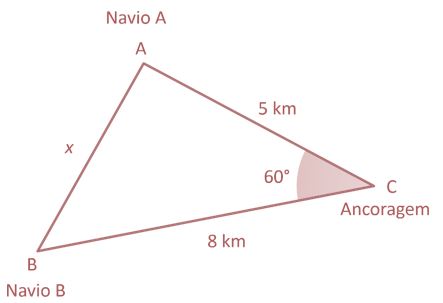
$latex \color{red}{{x}^{2}}={{5}^{2}}+{{8}^{2}}-2.5.8.\cos 60\Rightarrow \\{{x}^{2}}=25+64-80.0,5=49\Rightarrow x=7$
Questão 05 – 2ª Etapa
Um contêiner marítimo, usado para armazenamento, tem formato de um sólido geométrico. Os sólidos geométricos são compostos por três elementos: faces, arestas e vértices. As faces são constituídas por secções de planos; as arestas são os segmentos de retas entre as faces; os vértices estão nas extremidades das arestas. Um tubo deverá ser transportado neste contêiner. O mesmo será colocado diagonalmente no contêiner, partindo do vértice superior A ao vértice inferior B, conforme mostra a figura a seguir.

Nessas condições,
a) determine a expressão algébrica para calcular a diagonal do sólido.
b) usando as dimensões dadas na figura, calcule o comprimento máximo que um tubo pode ter, para que seja armazenado na diagonal do contêiner, desprezando o diâmetro do tubo, e que esse possa ser transportado com contêiner fechado.
Resposta
a) De modo geral, podemos encontrar o desenvolvimento de expressão algébrica que satisfaça a situação, ilustrando o paralelepípedo, teremos:
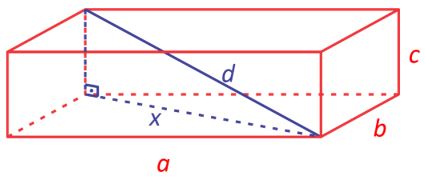
Usando a diagonal x na base do prisma e a diagonal que liga o vértice da base superior com o vértice oposto da base inferior:
$latex \color{red}\left\{ \begin{array}{l}{{x}^{2}}={{b}^{2}}+{{a}^{2}}\\{{d}^{2}}={{x}^{2}}+{{c}^{2}}\end{array} \right.$
Somando as duas equações, teremos:
$latex \color{red}\cancel{{{{x}^{2}}}}+{{d}^{2}}={{b}^{2}}+{{a}^{2}}+\cancel{{{{x}^{2}}}}+{{c}^{2}}\Rightarrow \\{{d}^{2}}={{b}^{2}}+{{a}^{2}}+{{c}^{2}}\Rightarrow d=\sqrt{{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}}$
Para mais conteúdo da UEMA, clique aqui.