[latexpage]
Fique com a prova resolvida da UEMA 2018. Em cada questão temos a resposta comentada.
Para mais conteúdo sobre a UEMA, clique aqui.
Questão 46 – 1ª Etapa
Um candidato necessita medir o tempo gasto no percurso do retorno da Forquilha até a UEMA para que, no dia do exame de vestibular, ele não se atrase para o início da prova. Veja no mapa o trajeto escolhido por ele.
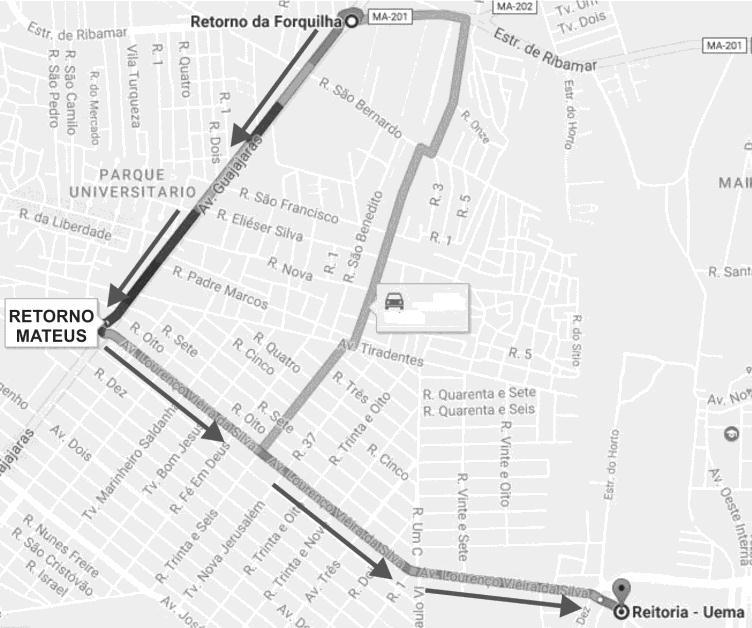
Considere que o candidato percorreu todo o trecho com os semáforos abertos, com pista livre e velocidade constante. Analise na tabela alguns dados deste percurso.
| Trecho percorrido | Distância Aproximada (km) | Velocidade km/h |
| Forquilha – Retorno Mateus | 2,1 | 54 |
| Retorno Mateus – UEMA | 2,4 | 36 |
O tempo gasto, em segundos, pelo candidato em todo o percurso foi de
a) 40
b) 104
c) 360
d) 370
e) 380
Resposta
Como as distâncias estão em decimais e o próprio exercícios pede a resposta em segundos:
2,1km = 2100m e 2,4km = 2400m
54km/h = 15m/s e 36km/h = 10m/s
1º Percurso: $\color{red} \frac{{15}}{1} = \frac{{2100}}{x} \Rightarrow 140s$
2º Percurso: $\color{red}\frac{{10}}{1} = \frac{{2400}}{x} \Rightarrow 240s$
Total = 140 + 240 = 380
Letra E
Questão 47 – 1ª Etapa
O anúncio a seguir é referente ao Imposto Territorial Urbano-IPTU de São Luís-MA, ano de 2017. Analise-o para responder à questão:

Considere uma residência cujo IPTU, relativo ao ano corrente, esteja estipulado em RS 425,00. Seu proprietário decidiu pagar esse tributo, antes de 05/07/2017, para ser beneficiado com o desconto ofertado, conforme anúncio supracitado. O valor pago pelo IPTU dessa residência, com o desconto oferecido, foi de
a) RS 63,75
b) RS 354,17
c) RS 361,25
d) RS 399,50
e) RS 488,75
Resposta
$\color{red}425 – \frac{{{{15}^{:5}}}}{{{{100}_{:5}}}}.425 = 425 – \frac{3}{{20}}.425 =$
$\color{red}425 – 3.21,25 = 425 – {\rm{63}}{\rm{,75}} = {\rm{361}}{\rm{,25}}$
Letra C
Questão 48 – 1ª Etapa
O infográfico a seguir representa o número de pessoas desocupadas, em milhões, por trimestre, começando (da esquerda para direita) no primeiro trimestre de 2016 até o primeiro trimestre de 2017. Analise–o para responder à questão.
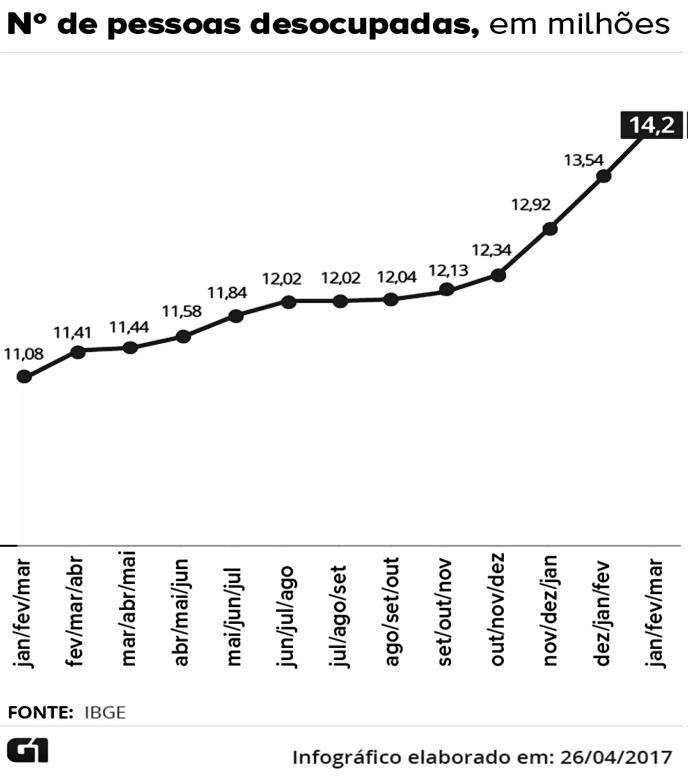
Ao se comparar o trimestre out/nov/dez de 2016 com o trimestre jan/fev/mar de 2017, o aumento do número de pessoas desempregadas é igual a
a) 660.000
b) 1.260.000
c) 1.280.000
d) 1.860.000
e) 2.160.000
Resposta
12,34 milhões = 12 340 000
14,2 milhões = 14 200 000
14 200 000 – 12 340 000 = 1 860 000
Letra D
Questão 49 – 1ª Etapa
Leia o seguinte texto sobre marés para responder à questão. As marés são movimentos de fluxo e de refluxo das águas dos mares provocados pela atração que a Lua e secundariamente o Sol exercem sobre os oceanos. Uma maré é bem semelhante à outra.
Do seu nível mais baixo, conhecida como maré baixa, a água sobe gradualmente por cerca de 6 horas até atingir a maré alta ou preamar. Daí então principia a baixar, continuando por cerca de 6 horas até alcançar a maré baixa ou baixa-mar. O ciclo então começa novamente. A diferença entre a maré alta e a maré baixa é chamada amplitude da maré.
Em certo dia do ano, a altura da maré, em metros, registrada no Porto do Itaqui, pode ser obtida, aproximadamente, pela fórmula:
$A\left( t \right) = 4 + 1.1sen\left\{ {\frac{\pi }{6}\left( {t + 2} \right)} \right\}$
Em que t representa o número de horas decorridas após a meia noite desse dia. A amplitude, em metros, da maré, nesse dia, foi de
a) 2,20
b) 2,10
c) 2,00
d) 1,65
e) 1,10
Resposta
Questão anulada com erro na grafia da fórmula A(t).
Questão 50 – 1ª Etapa
Muitas vezes, em nosso dia a dia, quando queremos resfriar algo rapidamente, colocamos o recipiente que o contém imerso em água fria. Tal situação é um exemplo da lei do resfriamento de Newton. Ela estabelece que, quando um corpo é colocado em um ambiente mantido à temperatura constante, sua temperatura varia de modo a ser a mesma do ambiente, a uma taxa proporcional à diferença de temperatura entre o corpo e o ambiente.
Assim, se T(t) representa a temperatura de um corpo no instante t > 0, com t em minutos, e Tm(t) é a temperatura do meio em torno desse corpo, tem-se que a formulação matemática dessa lei é:
$T\left( t \right) = {T_m}\left( t \right) + C.{e^{k\,t}}$, onde k e C são constantes reais.
Considere que um termômetro é retirado de um local com temperatura de 70°C e colocado em um ambiente com temperatura de 10°C. Após 30 segundos, esse termômetro indica 50°C. (Dados: ln 2 = 0,693, ln 3 = 1,098 e ln 6 =1,791; usar para o tempo a aproximação com duas casas decimais).
O tempo, em minutos, necessário para que esse termômetro marque 20°C é, aproximadamente, de
a) 0,81
b) 1,35
c) 2,21
d) 4,42
e) 132,66
Resposta
Primeiro encontraremos o valor de C. Tendo em vista que T(t) = 70, Tm(t) = 10° e t = 0.
$\color{red}70 = 10 + C.{e^{k.0}} \Rightarrow C = 60$
Agora, com a segunda situação iremos encontrar o valor de k:
$\color{red}50 = 10 + 60.{e^{k/2}} \Rightarrow 40 = 60.{e^{k/2}} \Rightarrow $
$\color{red}\ln \left( {\frac{2}{3}} \right) = \ln \left( {{e^{k/2}}} \right) \Rightarrow \ln 2 – \ln 3 = \frac{k}{2} \Rightarrow $
$\color{red}0,693 – 1,098 = \frac{k}{2} \Rightarrow k = – 0,81$
Resolvendo o questionamento:
$\color{red}20 = 10 + 60.{e^{ – 0,81.t}} \Rightarrow 10 = 60.{e^{ – 0,81.t}} \Rightarrow $
$\color{red}{e^{ – 0,81.t}} = \frac{1}{6} \Rightarrow \ln \left( {{e^{ – 0,81.t}}} \right) = \ln \left( {\frac{1}{6}} \right) \Rightarrow $
$\color{red} – 0,81t = \ln 1 – \ln 6 – 0,81t = – 1,791 \Rightarrow t = 2,21…$
Letra C
Para mais conteúdo sobre a UEMA, clique aqui.
Questão 01 – 2ª Etapa
Um funcionário de uma empresa agropecuária, no ato da sua contratação, precisa escolher entre duas propostas de plano de saúde com coparticipação. Nesse tipo de plano de saúde, além da mensalidade fixa, deve ser paga uma taxa no momento da consulta médica, de acordo com o contrato. Veja as propostas apresentadas a ele.
| Propostas | Valor fixo da mensalidade RS | Valor por consulta médica RS |
| A | 205,00 | 25,00 |
| B | 245,00 | 10,00 |
Determine qual dos dois planos é mais vantajoso para o funcionário, supondo que ele fará duas consultas médicas por mês. Justifique.
Resposta
Para a proposta A, teremos:
A = 205 + 25.2 = 255
Para a proposta B, teremos:
B = 245 + 10.2 = 265
O plano mais vantajoso é o plano A.
Questão 02 – 2ª Etapa
O Maranhão terá na colheita 2016/17 um aumento significativo na produção de grãos, segundo o sexto levantamento da Companhia Nacional de Abastecimento (CONAB) sobre a safra agrícola anterior. Com isto, o estado volta a ser o segundo maior produtor na região do Matopiba.
De acordo com o levantamento da CONAB, dois fatores contribuíram para esse aumento: 1) a ampliação da área plantada, saindo de 1,420 milhão para 1,655 milhão de hectares e 2) a produtividade que passou de 1748 quilos por hectare na colheita anterior para 2825 quilos por hectare nessa colheita. Esses fatores são explicados tanto pelo uso de novas tecnologias quanto por uma queda nas perdas, já que a safra passada foi marcada por um dos períodos de seca mais intensa no estado.
Com base nesses dados, calcule a quantidade de grãos prevista, em toneladas, para a colheita 2016/17.
Resposta
Área plantada: 1,655 milhão de hectares = 1 655 000 há
Produtividade: 2825 kg por hectare
Quantidade de grãos prevista: 1 655 000 x 2825 = 4 675 375 000 kg
Como 1 tonelada = 1000 kg
4 675 375 000 kg = 4 675 375 toneladas
Questão 03 – 2ª Etapa
A tabela a seguir mostra a distribuição dos salários mensais dos empregados de uma agropecuária nordestina.
| SALÁRIO (RS) | NÚMERO DE FUNCIONÁRIOS |
| 940,00 | 18 |
| 1600,00 | 12 |
| 2000,00 | 14 |
| 3000,00 | 12 |
| 4000,00 | 4 |
| 5000,00 | 3 |
| 8000,00 | 1 |
Com base nos dados dessa tabela, calcule a porcentagem de funcionários que recebem abaixo da média salarial dessa empresa.
Resposta
Fazendo o cálculo da média salarial, teremos:
$\color{red}\frac{{940.18 + 1600.12 + 2000.14 + 3000.12 + 4000.4 + 5000.3 + 8000}}{{18 + 12 + 14 + 12 + 4 + 3 + 1}}$
$\color{red}\frac{{16920 + 19200 + 28000 + 36000 + 16000 + 15000 + 8000}}{{64}}$
$\color{red}\frac{{139120}}{{64}} = 2173,75$
O número de funcionários que recebem abaixo da média: 14 + 12 + 18 = 44. O percentual será:
$\color{red}\frac{{44}}{{64}} = 0,68750 = 68,75\% $
Questão 04 – 2ª Etapa
O índice pluviométrico é utilizado para medir a quantidade de chuva, em milímetros, em determinado período de tempo. Seu cálculo é feito de acordo com o nível da água da chuva acumulada em um tanque aberto, em formato de um cubo, tendo uma base com 1 metro quadrado de área. Se o índice for de 30 milímetros, significa que a altura do nível de água acumulada nesse tanque mede 30 milímetros.
Um forte temporal estava prestes a acontecer. Marcos, desejando medir o índice pluviométrico, colocou uma lata, sem tampa, em formato cilíndrico de raio 300 milímetros no jardim de sua casa. Ao final da chuva, ele verificou que a altura da água, dentro da lata, era de 50 milímetros.
Calcule o índice pluviométrico encontrado por Marcos nesse temporal. Utilize 3,14 como aproximação de π.
Resposta
Ilustrando a situação, temos a figura abaixo:
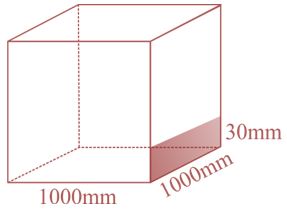
Vemos que o índice pluviométrico de 1mm é dado por 1000mm.1000mm.1mm = 1 000 000 mm³.
Na lata de Marcos, teremos:
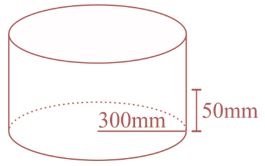
$\color{red}V = \pi \cdot {r^2} \cdot 50 = 3,14 \cdot {300^2} \cdot 50 = {\rm{14130000m}}{{\rm{m}}^3}$
Portanto, 14 130 000 mm³ na lata de Marcos correspondem ao índice pluviométrico de:
$\color{red}\frac{{14130000}}{{1000000}} = 14,13mm$
Questão 05 – 2ª Etapa
A falta de rede de esgoto nas zonas rurais é um grande problema de saúde pública. Muitas propriedades rurais têm fossas rudimentares, que são, apenas, buracos para receber os dejetos. O problema dessas fossas é que elas contribuem para a contaminação do lençol freático e os vírus e as bactérias presentes no material chegam aos poços que abastecem as casas e as plantações. As consequências desse ciclo são as doenças causadas por bactérias fecais, que se espalham rapidamente pela água. Em lugares onde não existe rede pública de abastecimento de água, é comum obter-se água no domicílio através de métodos paliativos tais como: poços comuns, semiartesiano, artesiano, fontes/minas, entre outras.
Deve-se respeitar por medida de segurança, a distância mínima de 15 metros, entre o poço e qualquer tipo de fossa e de 45 metros dos demais focos de contaminação, como chiqueiros, estábulos, valões de esgotos, galeria de infiltração e outros, que possam comprometer o lençol d’água que alimenta o poço.
Em uma propriedade rural, deseja-se construir uma residência (ponto A), implantar um poço artesiano (ponto B) e um local de coleta de esgoto (ponto C).
Após o reconhecimento da área, o técnico responsável pela construção optou por um modelo matemático triangular, com os seguintes dados: a distância entre B e C é 1 km, o ângulo entre os lados $\overline {AB} $ e $\overline {BC} $ é 105° e o ângulo entre os lados $\overline {AB} $ e $\overline {AC} $ é 30°.
Ilustre a situação com um desenho. A seguir, calcule a distância, em metros, da residência até o poço artesiano. Use $\sqrt 2 = 1,41$.
Resposta
Ilustrando a situação e transformando 1km em 1000 m, teremos:
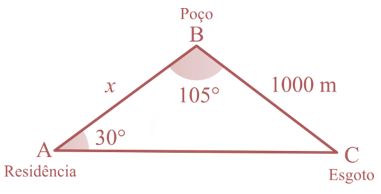
Como a soma dos ângulos internos de um triângulo é igual a 180°, temos que o ângulo C = 45° . Usaremos a lei dos senos:
$\color{red}\frac{{sen\hat C}}{x} = \frac{{sen30^\circ }}{{1000}} \Rightarrow \frac{{sen45^\circ }}{x} = \frac{{sen30^\circ }}{{1000}} \Rightarrow $
$\color{red}\frac{{\frac{{\sqrt 2 }}{2}}}{x} = \frac{{\frac{1}{2}}}{{1000}} \Rightarrow \frac{{\sqrt 2 }}{2} \cdot \frac{1}{x} = \frac{1}{2} \cdot \frac{1}{{1000}} \Rightarrow \frac{{\sqrt 2 }}{{2x}} = \frac{1}{{2000}}$
$\color{red}2x = 2000 \cdot \sqrt 2 \Rightarrow x = \frac{{2000 \cdot 1,41}}{2} \Rightarrow x = 1410m$
Questão 06 – 2ª Etapa
As cônicas são curvas no plano, obtidas pela interseção de um plano com um cone circular reto, dependendo da forma como essa interseção aconteça. No caso de o plano ser inclinado ao eixo do cone, não passar pelo vértice e, não ser paralelo a nenhuma das geratrizes, obtém–se a elipse, conforme figura a seguir.
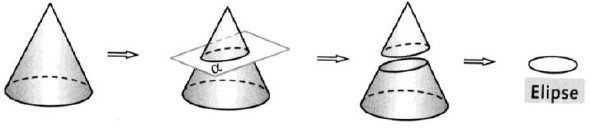
A elipse é responsável por modelar diversos problemas:
1) espelhos dos dentistas – a forma elíptica desses espelhos faz com que os raios de luz se concentrem no dente a ser tratado, facilitando a visualização pelo odontólogo e evitando o desconforto de ser o paciente ofuscado pelo fecho de luz;
2) aparelhos de radioterapia e outros – nos tratamentos radioterápicos, as células doentes são eliminadas enquanto células sadias ao seu redor não são afetadas;
3) utilização na Astronomia – os Planetas descrevem uma trajetória semelhante a uma elipse, tendo o sol como um dos focos.
Considere a elipse representada pela equação $4{x^2} + 9{y^2} – 32x – 54y + 109 = 0$. Calcule o centro, o comprimento do eixo maior, o comprimento do eixo menor. Em seguida, esboce o gráfico da elipse.
Resposta
O primeiro ponto será encontrar a equação reduzida da elipse:
$\color{red}4{x^2} + 9{y^2} – 32x – 54y + 109 = 0$
$\color{red}4{x^2} – 32x + 9{y^2} – 54y = – 109$
Para completarmos os quadrados perfeitos, adicionaremos 8² e 9²
$\color{red}\left[ {{{\left( {2x} \right)}^2} – 32x + {8^2}} \right] + \left[ {{{\left( {3y} \right)}^2} – 54y + {9^2}} \right] = – 109 + {8^2} + {9^2}$
$\color{red}{\left[ {2x – 8} \right]^2} + {\left[ {3y – 9} \right]^2} = 36$
$\color{red}{\left[ {2 \cdot \left( {x – 4} \right)} \right]^2} + {\left[ {3 \cdot \left( {y – 3} \right)} \right]^2} = 36$
$\color{red}4 \cdot {\left( {x – 4} \right)^2} + 9 \cdot {\left( {y – 3} \right)^2} = 36$
$\color{red}\frac{{4.{{\left( {x – 4} \right)}^2} + 9.{{\left( {y – 3} \right)}^2} = 36}}{{36}}$
$\color{red}\frac{{{{\left( {x – 4} \right)}^2}}}{9} + \frac{{{{\left( {y – 3} \right)}^2}}}{4} = 1$
Agora, podemos ver que esta elipse não possui centro na origem. Lembre–se que:
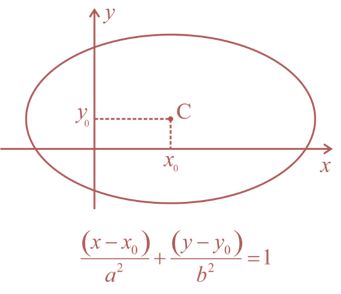
Teremos o C = (4,3). Lembrando novamente:
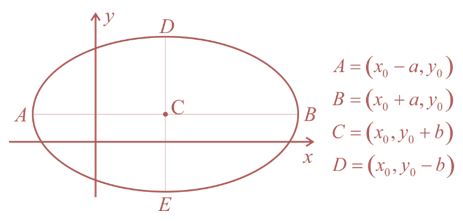
Vamos ao cálculo:
$\color{red}\left[\kern-0.15em\left[ \begin{array}{l}
A = \left( {4 – 3,3} \right) = \left( {1,3} \right)\\
B = \left( {4 + 3,3} \right) = \left( {7,3} \right)
\end{array}
\right]\kern-0.15em\right] \Rightarrow AB = 6$
Esboçando, até que enfim, o gráfico:
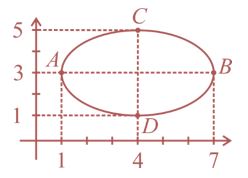
Para mais conteúdo sobre a UEMA, clique aqui.