[latexpage] Separamos os exercícios de matemática da UEMA resolvidos dos temas mais frequentes nas provas.
Com as questões é possível conhecer o estilo da banca. Com isso, o candidato tem maior eficiência nos seus estudos, assimilando os conteúdos essenciais e poupando seu valioso tempo.

Mais abaixo temos questões dos conteúdos que mais caíram no vestibular da UEMA.
📝 Operações Básicas
Questão 01
(UEMA) Um carro–tanque chega a um posto de venda de combustível com uma carga de 24.300 litros de gasolina que deverá ser descarregada no reservatório desse posto, na base de 900 litros por minuto. Após 12 minutos do início dessa operação, quantos litros de gasolina ainda restavam no carro–tanque?
a) 10.800 litros.
b) 13.500 litros.
c) 12.150 litros.
d) 9.000 litros.
e) 9.900 litros
Resposta
Após 12 minutos, teremos 12.900 = 10 800 litros descarregados
Assim, restavam 24 300 – 10 800 = 13 500 litros
Letra B
Questão 02
(UEMA) O Maranhão terá na colheita 2016/17 um aumento significativo na produção de grãos, segundo o sexto levantamento da Companhia Nacional de Abastecimento (CONAB) sobre a safra agrícola anterior. Com isto, o estado volta a ser o segundo maior produtor na região do Matopiba. De acordo com o levantamento da CONAB, dois fatores contribuíram para esse aumento: 1) a ampliação da área plantada, saindo de 1,420 milhão para 1,655 milhão de hectares e 2) a produtividade que passou de 1748 quilos por hectare na colheita anterior para 2825 quilos por hectare nessa colheita. Esses fatores são explicados tanto pelo uso de novas tecnologias quanto por uma queda nas perdas, já que a safra passada foi marcada por um dos períodos de seca mais intensa no estado.
Com base nesses dados, calcule a quantidade de grãos prevista, em toneladas, para a colheita 2016/17.
Resposta
Área plantada: 1,655 milhão de hectares = 1 655 000 há
Produtividade: 2825 kg por hectare
Quantidade de grãos prevista: 1 655 000 x 2825 = 4 675 375 000 kg
Como 1 tonelada = 1000 kg
4 675 375 000 kg = 4 675 375 toneladas
📝 Frações
Questão 03
(UEMA) Um pai deixou um testamento no qual a sua herança será dividida pelos três filhos da seguinte forma: o primeiro deverá receber 1/3 da herança; o segundo 2/5 e o restante ficará para o terceiro filho. Qual o percentual da herança que cabe ao terceiro filho?
a) 7/15 da herança;
b) 11/15 da herança;
c) 2/15 da herança;
d) 8/15 da herança;
e) 4/15 da herança;
Resposta
Somando as partes dos dois primeiros temos: $ \color{red} \left( {\frac{1}{3} + \frac{2}{5} = \frac{{5 + 6}}{{15}} = \frac{{11}}{{15}}} \right)$
Agora falta o terceiro! Vamos considerar o todo como sendo $ \color{red} \frac{{15}}{{15}}$.
A terceira parte x será: $ \color{red} x = \frac{{15}}{{15}} – \frac{{11}}{{15}} = \frac{4}{{15}}$.
Letra E
Acesse o curso gratuito de Matemática Básica

Com foco total no vestibular da UEMA
📝 Razões e proporções
Questão 04
(UEMA) Analise a situação abaixo:
A atleta maranhense Júlia Nina, do MAC/Nina, teve ótima performance nas águas do Lago Paranoá, em Brasília/DF e conquistou a medalha de ouro na disputa da 4ª etapa do Circuito Brasileiro de Maratonas Aquáticas. Com apenas 13 anos, a atleta vem contabilizando importantes resultados em níveis nacional e internacional. Obteve o seu bicampeonato na categoria Infantil com o tempo de 2h25min24seg. A marca obtida na prova dos 10km ainda rendeu à Júlia o sétimo lugar na categoria Absoluto. O valor aproximado da velocidade média, em m/s, imposta pela atleta, no cumprimento da prova, é de
a) 1,27
b) 1,39
c) 1,50
d) 1,15
e) 1,20
Resposta
O tempo total, em segundos da atleta foi de:
2 horas = 120 minutos = 7200 segundos
25 minutos = 1500 segundos
Assim, o tempo total em segundos: 7200 + 1500 + 24 = 8724.
Como 10km = 10000 metros:
A velocidade V será $ \color{red} V = \frac{{10000}}{{8724}} \cong 1,15$
Letra D
Questão 05
(UEMA) O quadro ao lado representa o custo médio mensal de ração para cães em um hotel. Um casal adulto da raça Boxer e uma cadela adulta da raça Yorkshire ficarão dois meses no hotel para cães. O custo médio das rações consumidas pelos cães representa 34% da mensalidade a ser paga. O gasto total, em reais, por um período de dois meses, será de
a) RS 500,00
b) RS 800,00
c) RS 1.000,00
d) RS 971,42
e) RS 790,70
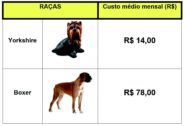
Resposta
Para um casal da raça Boxer, 2.78 = 156
Para uma cadela da raça Yorkshire 14.
Com ração, teremos o gasto de 156 + 14 = 170.
Esse gasto representa 34% da mensalidade m: $\color{red}170= \frac{{34}}{{100}}m=\frac{{17000}}{{34}}=m=500 $
Para dois meses: 2.500 = 1000
Letra C
📝 Equações e sistemas
Questão 06
(UEMA) Uma comunidade do interior do estado decidiu construir uma creche por meio de doações. O projeto da creche descreve que serão necessários 300 m² de parede. O projetista informou que, para cada metro quadrado de parede, são necessários 32 tijolos cerâmicos de 6 furos, considerando a espessura da massa de cimento. As doações dos tijolos aconteceram da seguinte forma:
Morador A – doou x tijolos.
Morador B – doou o dobro de tijolos do morador A.
Morador C – doou 1.000 tijolos a menos que o morador B.
A quantidade individual de tijolos doada pelo morador C e o total necessário para a construção da creche são, respectivamente,
a) 5.000 e 14.000
b) 1.440 e 9.600
c) 3.240 e 9.600
d) 3.000 e 14.000
e) 2.120 e 9.600
Resposta
De acordo com as especificações, teremos o total de tijolos sendo:
300.32 = 9600.
Agora, usando as informações:
Morador A – doou x tijolos (x)
Morador B – doou o dobro de tijolos do morador A (2x)
Morador C – doou 1.000 tijolos a menos que o morador B (2x – 1000)
Montando a equação, teremos:
x + 2x + 2x – 1000 = 9600 ⟹ x = 2120
Assim, o morador C = 2x – 1000 = 2.2120 – 1000 = 3240
Letra C
Questão 07
(UEMA) Uma consultora de produtos de beleza precisa repor o seu estoque junto à distribuidora. Para tanto, gastou nas suas compras RS 345,00 para a reposição do estoque cujos preços, por unidade, são: RS 12,00, o batom e RS 7,00, o esmalte. Sabendo que foram adquiridas 35 unidades de produtos no total, calcule a quantidade de batons e de esmaltes comprados.
Resposta
Montaremos um sistema sendo b o número de batons e e o número de esmaltes
b + e = 35
12b + 7e = 345
Agora, multiplicando a primeira equação por -7:
-7b – 7e = -245
12b + 7e = 345
Resolvendo pelo método aditivo:
b = 20 e e = 15
📝 Geometria Plana
Questão 08
(UEMA) A figura abaixo representa uma quadra de futebol de salão com a bola localizada no ponto P, conforme descrito na figura de vértice ABCD. No ponto C, há um jogador que receberá a bola chutada a partir de onde ele está. Determine a distância x do jogador (ponto C) à bola (ponto P) em unidade de comprimento.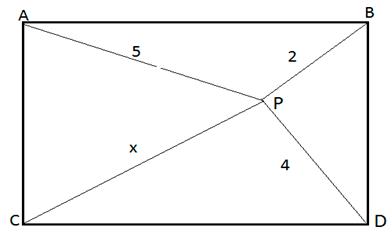
Resposta
Vamos desconsiderar o erro de intersecção do ponto P e traçaremos a altura do triângulo APB e a altura do triângulo CPD: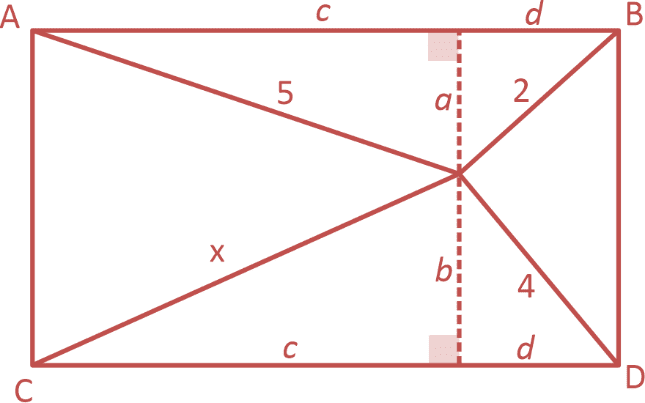
Agora, aplicaremos uma sequência dinamitadora” de Pitágoras:
$\color{red}\left\{ \begin{array}{lI}{{a}^{2}}+{{c}^{2}}=25\\{{a}^{2}}+{{d}^{2}}=4\\{{b}^{2}}+{{c}^{2}}={{x}^{2}}\\{{b}^{2}}+{{d}^{2}}=16\end{array} \right$
e somando todas as equações:
$latex \color{red} \begin{array}{c}2{{a}^{2}}+2{{b}^{2}}+2{{c}^{2}}+2{{d}^{2}}=45+{{x}^{2}}\Rightarrow \\2\left( {{{a}^{2}}+{{c}^{2}}} \right)+2\left( {{{b}^{2}}+{{d}^{2}}} \right)=45+{{x}^{2}}\Rightarrow \\2.25+2.16=45+{{x}^{2}}\\50+32-45={{x}^{2}}=37\Rightarrow x=\sqrt{{37}}\end{array}$
Questão 09
(UEMA) Gabrielle e sua família mudaram-se para uma casa nova. Ao saber que teria seu próprio quarto, Gabrielle tratou de decorar, com papel de parede, o lado em que fica a janela. Pesquisou, na planta, as dimensões do quarto e observou que essa parede possui 2,50m x 2,80m.
Sabendo-se que a janela mede 1m x 1,20m, a quantidade de papel de parede, em metros quadrados, a ser utilizada para a decoração é de
a) 5,5
b) 5,8
c) 6,3
d) 7,0
e) 8,2
Resposta
A área da parede será 2,5m.2,8m = 7m²
A área da janela será 1m.1,2m = 1,2m²
A quantidade de papel de parede será: 7m² – 1,2m² = 5,8 m²
Letra B
Questão 10
(UEMA) Uma pista de atletismo será construída na cidade ABC em torno de um terreno formado por um retângulo (campo de futebol) com 100 metros de comprimento e 72 metros de largura e duas semicircunferências cujo diâmetro coincide com a largura da área retangular. Observe a figura a seguir: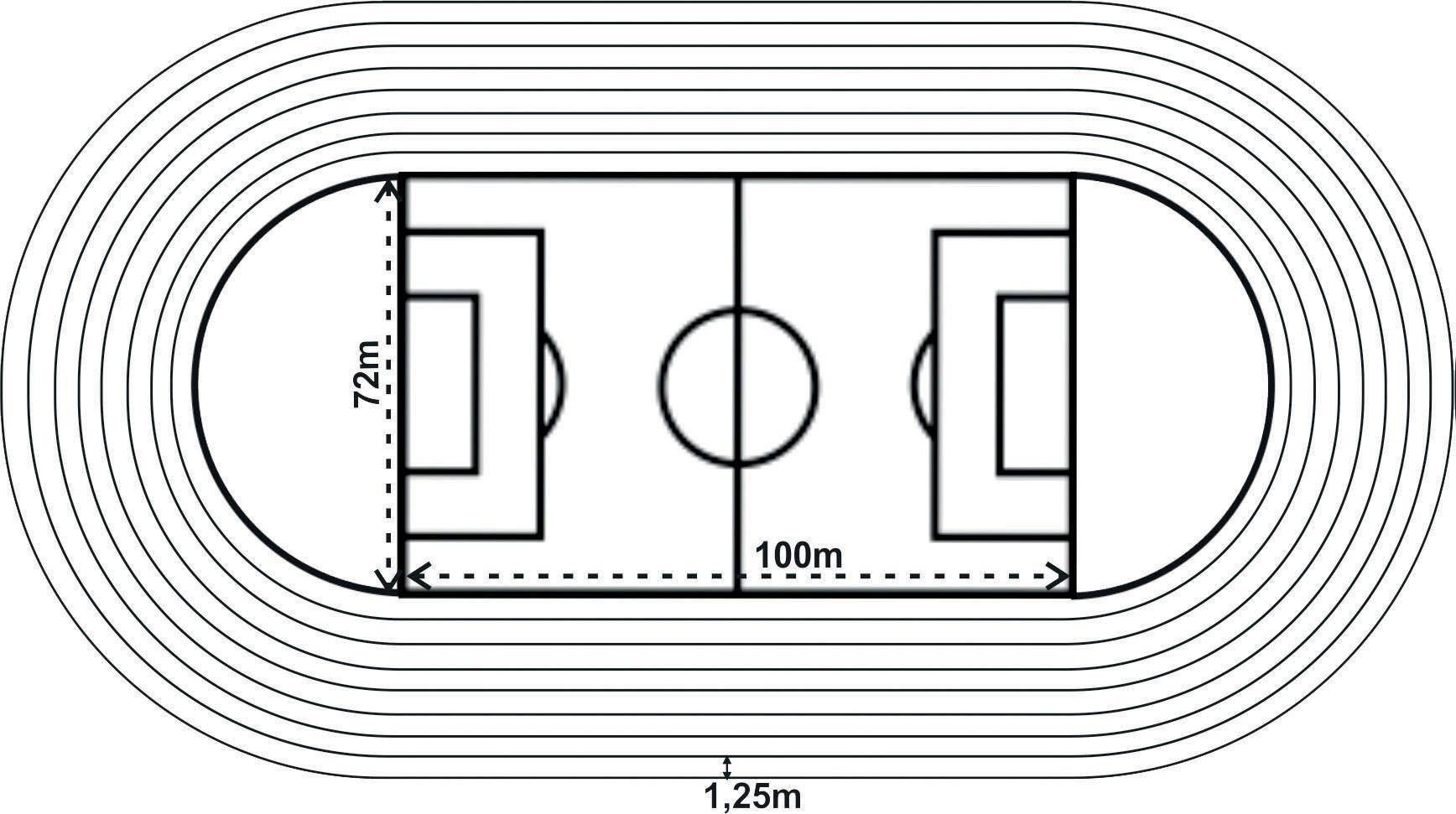
O prefeito da cidade ABC deseja revestir essa pista de atletismo, e a empreiteira que ganhou a licitação cobrará RS 120, 00 por metro quadrado aplicado de revestimento. A pista terá 8 raias (são os caminhos pelos quais os atletas devem correr) de 1,25 metros de largura cada uma.
Calcule o preço total gasto para revestir toda essa pista. Considere π =3,14.
Resposta
A largura total da pista será 8.1,25 = 10m.
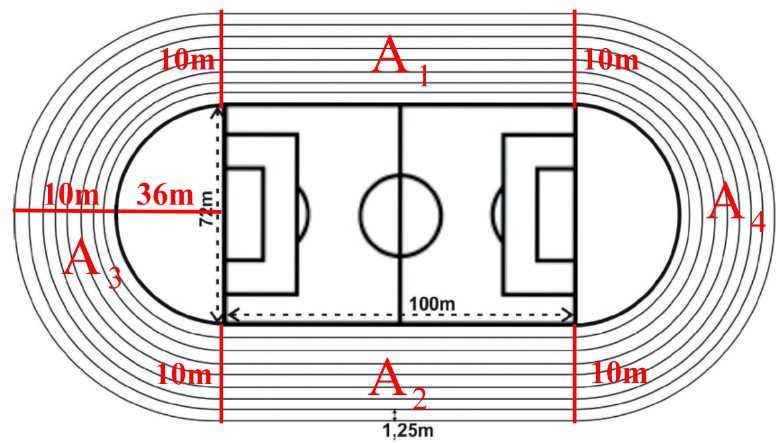
$\color{red}\begin{array}{l}
{A_1} + {A_2} = 2.10.100 = 2000{m^2}\\
{A_3} + {A_4} = \pi {.46^2} – \pi {.36^2} = 3,14.\left( {{{46}^2} – {{36}^2}} \right) = \\
3,14.\left( {46 – 36} \right)\left( {46 + 36} \right) = 3,14.10.82 = 2574,8{m^2}
\end{array}$
Somando: $\color{red}{A_1} + {A_2} + {A_3} + {A_4} = 4{\rm{574}}{\rm{,8}}{{\rm{m}}^2}$
Gasto: 4574,8.120 = RS 548 976,00
📝 Geometria espacial (sólidos geométricos)
Questão 11
(UEMA) Um contêiner marítimo, usado para armazenamento, tem formato de um sólido geométrico. Os sólidos geométricos são compostos por três elementos: faces, arestas e vértices. As faces são constituídas por secções de planos; as arestas são os segmentos de retas entre as faces; os vértices estão nas extremidades das arestas. Um tubo deverá ser transportado neste contêiner. O mesmo será colocado diagonalmente no contêiner, partindo do vértice superior A ao vértice inferior B, conforme mostra a figura a seguir.
a) determine a expressão algébrica para calcular a diagonal do sólido.
b) usando as dimensões dadas na figura, calcule o comprimento máximo que um tubo pode ter, para que seja armazenado na diagonal do contêiner, desprezando o diâmetro do tubo, e que esse possa ser transportado com contêiner fechado.
Resposta
a) De modo geral, podemos encontrar o desenvolvimento de expressão algébrica que satisfaça a situação, ilustrando o paralelepípedo, teremos:
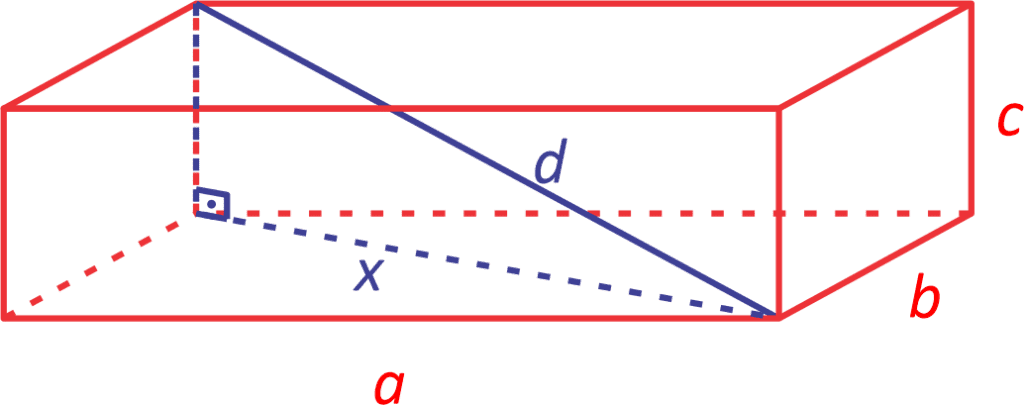
Usando a diagonal x na base do prisma e a diagonal que liga o vértice da base superior com o vértice oposto da base inferior:
$\color{red} \left\{ \begin{array}{l} {x^2} = {b^2} + {a^2}\\{d^2} = {x^2} + {c^2} \end{array} \right.$
Somando as duas equações, teremos:
$\color{red}\begin{array}{l}
\cancel{{{x^2}}} + {d^2} = {b^2} + {a^2} + \cancel{{{x^2}}} + {c^2}\\
{d^2} = {b^2} + {a^2} + {c^2} \Rightarrow d = \sqrt {{a^2} + {b^2} + {c^2}}
\end{array}$
b) $\color{red}\begin{array}{l}
T = \sqrt {{{\left( {2,1} \right)}^2} + {{\left( {5,3} \right)}^2} + {{\left( {2,2} \right)}^2}} = \\
\sqrt {4,41 + 28,09 + 4,84} = \sqrt {37,34} \cong 6
\end{array}$
Questão 12
(UEMA) Qualquer quantidade de água exposta sofrerá a evaporação, pois este é um processo natural físico. Com uma piscina não seria diferente: incidência constante de sol, de calor, de vento e de baixa umidade contribui para o nível da água abaixar diariamente. Entretanto, por experiências, se diz que há um limite máximo de aproximadamente 5 cm / semana ou 3 mm / dia de evaporação, que, obviamente, varia de acordo com o tamanho da superfície da piscina e de fatores meteorológicos, como os citados acima. Provavelmente, quando esses valores são ultrapassados, a piscina apresenta problemas de vazamento.
Tendo como foco uma piscina semiolímpica, de base retangular, com 25 m de comprimento, 20 m de largura e uma profundidade uniforme de 1,3 m (da lâmina d’água até o fundo da piscina), pergunta-se:
a) Considerando o limite de 5 cm por semana de evaporação, calcule a quantidade de litros de água que restará na piscina, após uma semana sem reposição alguma de água.
b) Considerando a evaporação de 3 mm por dia, calcule quantos litros de água deverão ser recolocados na piscina, após 12 dias, para que a piscina retorne ao nível de água inicial.
Resposta
a) Volume da Piscina:
V = 25.20.1,3 = 650m³ = 650000 dm³ = 650000 L
A evaporação corresponde: E = 25.20.0,05 = 25m³.
1m³ = 1000L
25m³ = 25000 L
Restam na piscina: 650000 – 25000 = 625000
b) A evaporação corresponde:
25.20.12.0,003 = 18m³ = 18000 dm³ = 18000 L
📝 Geometria Analítica
Questão 13
(UEMA) Buscando incentivar a inserção das pessoas com deficiência no mercado de trabalho, uma filial dos Correios da cidade de São Luís contratou um cadeirante como encarregado da separação de correspondências. Para executar este trabalho, o novo funcionário foi designado para uma sala que dispunha de três mesas. Suponha que os centros dessas mesas sejam representados pelos pontos A, B e C de coordenadas (5,4), (3,7) e (1,2), respectivamente, tomando como origem o canto da sala. Nessas condições,
a) esboce a figura que representa a disposição das mesas na sala em questão.
b) quais as distâncias que cada mesa mantém entre si, em metros?
c) qual a área do espaço compreendido entre as mesas?
Resposta
a) Colocando cada ponto no plano cartesiano, teremos:
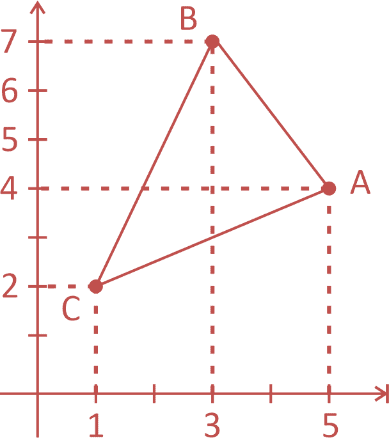
b) A distância das mesas A e B será:
$\color{red}{D_{AB}} = \sqrt {{{\left( {3 – 5} \right)}^2} + {{\left( {7 – 4} \right)}^2}} = \sqrt {4 + 9} = \sqrt {13} $
A distância das mesas B e C será:
$\color{red}{D_{BC}} = \sqrt {{{\left( {1 – 3} \right)}^2} + {{\left( {2 – 7} \right)}^2}} = \sqrt {4 + 25} = \sqrt {29}$
A distância das mesas A e C será:
$\color{red}{D_{AC}} = \sqrt {{{\left( {1 – 5} \right)}^2} + {{\left( {2 – 4} \right)}^2}} = \sqrt {16 + 4} = \sqrt {20} $
Questão 14
(UEMA) O método analítico em Geometria é uma ferramenta muito utilizada em estudo de coordenadas. Para fazer uma aplicação desse método, um professor lançou o seguinte desafio aos seus alunos: Teriam de construir, em sistema de coordenadas, a figura de um paralelogramo ABCD, cujo ponto A está na origem; o ponto D(5,0) e a diagonal maior com extremidade no ponto C(9,4). Com base nas informações,
a) faça o esboço em sistema de coordenadas da figura que representa o paralelogramo.
b) determine a equação da reta que contém a diagonal maior.
Resposta
a) Ilustrando a situação, temos a certeza que a ordenada do ponto D equivale a 4, já que o quadrilátero ABCD é paralelogramo. Todo paralelogramo possui lados opostos congruentes, portanto CD = AD = 5 obrigando a abscissa do ponto D ser igual a 4. Por fim, temos o ponto D(4,4).
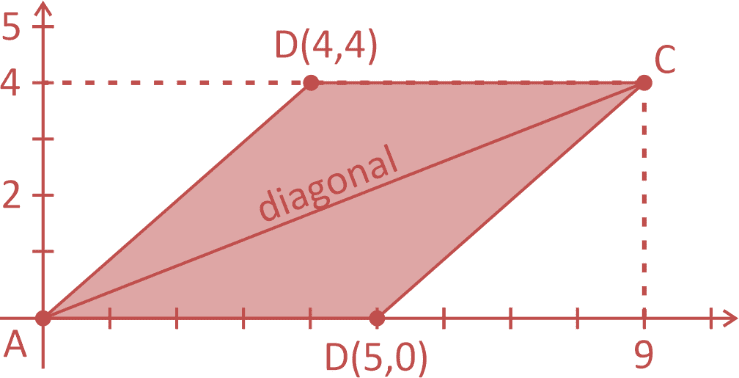
b) Calculando o coeficiente angular m:
$\color{red}m = \frac{{y – {y_0}}}{{x – {x_0}}} = \frac{{4 – 0}}{{9 – 0}} = \frac{4}{9}$
Escolhendo o ponto C(9,4) e usando a equação da reta $\color{red}y – {y_0} = m\left( {x – {x_0}} \right):$
$\color{red}\begin{array}{l}
y – {y_0} = m\left( {x – {x_0}} \right) \Rightarrow y – 4 = \frac{4}{9}\left( {x – 9} \right) \Rightarrow \\
9y – 36 = 4x – 36 \Rightarrow 9y = 4x \Rightarrow y = \frac{{4x}}{9}
\end{array}$
📝 Análise combinatória
Questão 15
(UEMA) A rádio comunitária de Santa Teresa anunciou que o PCL estava reunido para escolher 8 candidatos a vereador da cidade pelo partido para concorrer às próximas eleições. O partido dispõe de 13 candidatos a candidatos a vereador, sendo 3 mulheres e 10 homens. Segundo o regimento interno do partido, ao menos 25% dos candidatos do PCL são obrigatoriamente mulheres. O locutor da rádio ofereceu um prêmio a quem prever a lista com os 8 escolhidos. O Sr. Lourival foi o vencedor da premiação, pois ele listou todas as possíveis composições dos 8 candidatos, respeitando o regimento interno do partido. Quantas listas o Sr. Lourival enviou à rádio indicando os possíveis candidatos?
a) 882 listas
b) 1782 listas
c) 1287 listas
d) 462 listas
e) 630 listas
Resposta
A lista possuirá 8 escolhidos dentre eles ao menos 25% são mulheres. Portanto teremos duas situações a considerar:
1ª lista: duas mulheres (25% de 8)
2ª lista: três mulheres.
Para duas mulheres na lista:
Teremos que escolher duas mulheres em 3 disponíveis: $\color{red}{C_{3,2}}$ e escolher 6 homens em 10 disponíveis: $ \color{red}{C_{10,6}}$
Totalizando:
$ \color{red} {C_{3,2}}.{C_{10,6}} = \frac{{3!}}{{2!1!}}.\frac{{10!}}{{6!4!}} = \frac{{3.2.10.9.8.7.6!}}{{2.6!.4.3.2}} = 10.9.7 = 630$
Agora, para três mulheres na lista:
Teremos que escolher 3 mulheres em 3 disponíveis: $ \color{red} {C_{3,3}}$ e escolher 5 homens em 10 disponíveis: $\color{red} {C_{10,5}}$
Totalizando:
$ \color{red} {C_{3,2}}.{C_{10,5}} = 1.\frac{{10!}}{{5!5!}} = \frac{{10.9.8.7.6.5!}}{{5.4.3.2.5!}} = 2.9.2.7 = 252$
Somando, temos 630 + 252 = 882
📝 Análise de gráficos e tabelas
Questão 16
(UEMA) Uma empresa da construção civil faz 3 tipos de casa: tipo 1, para casal sem filhos; tipo 2, para casal com até 2 filhos e tipo 3, para casal com 3 ou mais filhos. A empresa de material de construção Barateiro Umbizal fornece ferro, madeira, telha e tijolo, para a primeira etapa da construção, conforme tabelas de material e de preço.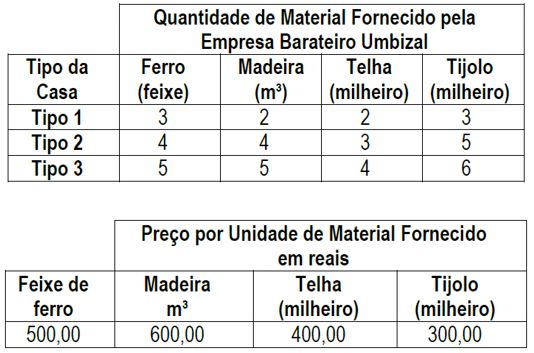
Sabendo que a empresa construirá 2, 4, e 5 casas dos tipos 1,2 e 3, respectivamente, o preço unitário de cada tipo de casa e o custo total do material fornecido, para esta primeira etapa de construção, pela empresa, em reais, é de
a) Tipo 1: 5.200; Tipo 2: 7.100; Tipo 3, 8.900; Custo Total: 83.300.
b) Tipo 1: 4.400; Tipo 2: 7.100; Tipo 3, 9.100; Custo Total: 82.700.
c) Tipo 1: 4.400; Tipo 2: 7.100; Tipo 3, 8.900; Custo Total: 81.700.
d) Tipo 1: 4.400; Tipo 2: 7.400; Tipo 3, 8.900; Custo Total: 82.900.
e) Tipo 1: 4.500; Tipo 2: 7.100; Tipo 3, 8.800; Custo Total: 82.400.
Resposta
Vamos calcular o preço unitário de casas do tipo 1:
3.500 + 2.600 + 2.400 + 3.300 = 1500 + 1200 + 800 + 900 = 2.3600 = 4 400
Vamos calcular o preço unitário de casas do tipo 2:
4.500 + 4.600 + 3.400 + 5.300 = 2000 + 2400 + 1200 + 1500 = 7 100
Vamos calcular o preço unitário de casas do tipo 3:
5.500 + 5.600 + 4.400 + 6.300 = 2500 + 3000 + 1600 + 1800 = 8 900
O custo para a construção das casas será:
2.4400 + 4.7100 + 5.8900 = 8800 + 28400 + 44500 = 81 700
Letra C