Fique com as questões da UEMA separadas por assunto. Em cada questão temos a resposta comentada. Abaixo temos as questões da Uema sobre operações elementares (soma, subtração, multiplicação e divisão).
Questão 1
Q24F (UEMA) Um professor de natação de uma escola ao realizar treinos com 3 de seus atletas,[…] uma determinada categoria, lançou um desafio: o vencedor seria o atleta que obtivesse a menor soma dos tempos (em segundos) nas três modalidades de nados–50m livre, 50m peito, 50m borboleta–nas duas últimas séries do treinamento. Os resultados obtidos nos diferentes tipos de nado estão especificados nos quadros abaixo:
| Penúltima série | Atleta 1 | Atleta 2 | Atleta 3 |
| 50m livre | 28 | 27 | 26 |
| 50m peito | 38 | 40 | 39 |
| 50m borboleta | 35 | 36 | 37 |
| Última série | Atleta 1 | Atleta 2 | Atleta 3 |
| 50m livre | 27 | 26 | 25 |
| 50m peito | 37 | 37 | 39 |
| 50m borboleta | 35 | 37 | 38 |
O atleta vencedor totalizou o tempo de:
a) 204 segundos.
b) 205 segundos.
c) 196 segundos.
d) 169 segundos.
e) 200 segundos.
Resposta
Somatório dos tempos do Atleta 1:
28 + 38 + 35 + 27 + 37 + 35 = 200
Somatório dos tempos do Atleta 2:
27 + 40 + 36 + 26 + 37 + 37 = 203
Somatório dos tempos do Atleta 3:
26 + 39 + 37 + 25 + 39 + 38 = 204
Assim, o vencedor foi o Atleta 1, com 200 segundos.
Letra E
Questão 2
Q1812F (UEMA) Durante longos períodos de quarentena, isolamento, distanciamento social e lockdown, com o objetivo de impedir ou amenizar a contaminação pelo COVID-19 (SARS-CoV-2), as centrais telefônicas se tornaram ainda mais importantes com o uso PABX VIRTUAL, pois as pessoas de cada Estado ou Cidade utilizam seus serviços para agendamento de consultas e de exames, sem saírem de casa.
Analise a seguinte situação-problema.
Uma Central de Marcação deixa em espera os clientes, à medida em que vai atendendo às ligações telefônicas. O tempo de atendimento de cada cliente dura 3 minutos. Considere que o último cliente ocupa a posição 40º (quadragésimo). Essa posição vai decrescendo, até atingir a posição da origem (zero), que representa o cliente que está sendo atendido.
Considerando as condições da situação-problema, o total de tempo gasto, em notação de horas e de minutos, para que todos os clientes sejam atendidos é de
a) 2 horas e 03 minutos.
b) 1 hora e 23 minutos.
c) 2 horas e 05 minutos.
d) 2 horas e 23 minutos.
e) 1 hora e 25 minutos.
Questão 3
Q54F (UEMA) Um carro–tanque chega a um posto de venda de combustível com uma carga de 24.300 litros de gasolina que deverá ser descarregada no reservatório desse posto, na base de 900 litros por minuto. Após 12 minutos do início dessa operação, quantos litros de gasolina ainda restavam no carro–tanque?
a) 10.800 litros.
b) 13.500 litros.
c) 12.150 litros.
d) 9.000 litros.
e) 9.900 litros.
Resposta
Após 12 minutos, teremos
12.900 = 10 800 litros descarregados
Assim, restavam
24 300–10 800 = 13 500 litros
Letra B
Questão 4
Q58F (UEMA) O Maranhão terá na colheita 2016/17 um aumento significativo na produção de grãos, segundo o sexto levantamento da Companhia Nacional de Abastecimento (CONAB) sobre a safra agrícola anterior. Com isto, o estado volta a ser o segundo maior produtor na região do Matopiba. De acordo com o levantamento da CONAB, dois fatores contribuíram para esse aumento:1) a ampliação da área plantada, saindo de 1,420 milhão para 1,655 milhão de hectares e 2) a produtividade que passou de 1748 quilos por hectare na colheita anterior para 2825 quilos por hectare nessa colheita. Esses fatores são explicados tanto pelo uso de novas tecnologias quanto por uma queda nas perdas, já que a safra passada foi marcada por um dos períodos de seca mais intensa no estado.
Com base nesses dados, calcule a quantidade de grãos prevista, em toneladas, para a colheita 2016/17.
Resposta
Área plantada:
1,655 milhão de hectares = 1 655 000 há
Produtividade: 2825 kg por hectare
Quantidade de grãos prevista:
1 655 000 x 2825 = 4 675 375 000 kg
Como 1 tonelada = 1000 kg
4 675 375 000 kg = 4 675 375 toneladas
Questão 5
Q59F (UEMA) Um funcionário de uma empresa agropecuária, no ato da sua contratação, precisa escolher entre duas propostas de plano de saúde com coparticipação. Nesse tipo de plano de saúde, além da mensalidade fixa, deve ser paga uma taxa no momento da consulta médica, de acordo como contrato. Veja as propostas apresentadas a ele.
| Propostas | Valor fixo da Mensalidade (R$) | Valor por Consulta Médica (R$) |
| A | 205,00 | 25,00 |
| B | 245,00 | 10,00 |
Determine qual dos dois planos é mais vantajoso para o funcionário, supondo que ele fará duas consultas médicas por mês. Justifique.
Resposta
Para a proposta A, teremos:
A = 205 + 25.2 = 255
Para a proposta B, teremos:
B= 245 + 10.2 = 265
O plano mais vantajoso é o plano A.
Questão 6
Q87F (UEMA) Uma das mais antigas máquinas de calcular é o ábaco. A seguir, veja a imagem de um ábaco, contendo a representação de um número N, com suas ordens (unidades, dezenas, centenas e unidade de milhar).
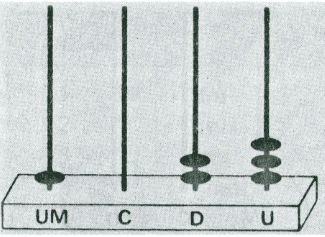
O resto da divisão desse número N por 37 é:
a) 24.
b) 42.
c) 23.
d) 29.
e) 19.
Resposta
O número mostrado pelo ábaco é 1023. Dividindo por 27
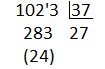
Letra A.
Para mais questões da UEMA por assunto clique aqui
Questão 7
Q72F (UEMA) Analise o gasto de três usuários de ônibus da ilha de SãoLuís – MA. O Sr. Pandolfo vai ao trabalho no ônibus da linha de Ribamar, paga R\$ 2,30 por passagem e percorre 11,5 km de sua casa ao trabalho. A Sra. Jaulina vai à aula de hidroginástica no ônibus da linha do Maiobão, paga R\$ 2,10 por passagem e percorre 14km. Dona Ambrosina vai ao teatro no ônibus do Caratatiua, paga R\$ 1,70 e percorre 5km. A afirmação correta, considerando o valor pago por cada usuário de ônibus e o quilômetro percorrido, é a seguinte:
a) Dona Jaulina paga R$ 0,20 por quilômetro percorrido.
b) o Sr. Pandolfo paga o menor valor por quilômetro percorrido.
c) Dona Ambrosina paga maior valor por quilômetro percorrido.
d) Dona Jaulina e o Sr. Pandolfo pagam juntos R$ 0,45 por quilômetro percorrido.
e) Dona Ambrosina e o Sr. Pandolfo pagam juntos R$ 0,60 por quilômetro percorrido.
Resposta
Veremos quanto o Sr. Pandolfo paga por km:
2,3 ÷ 11,5 = 0,2. R$ 0,20 por km.
Veremos quanto a Sra. Jaulina paga por km:
2,1 ÷ 14 = 0.15. R$ 0,15 por km.
Veremos quanto a Dona Ambrosina paga por km:
1,7 ÷ 5 = 0,34. R$ 0,34por km.
Letra C
Questão 8
Q73F (UEMA) A fim de realizar o pagamento de uma festa de formatura, estabeleceu–se um valor de R\$ 800,00 para cada aluno formando e mais um valor adicional por cada convidado. Considerandoque um formando convidou 8 pessoas, tendo despendido o total de R\$ 1.200,00, determine o valorpago por esse formando por cada convidado.
Resposta
Calculando o valor adicional:
1200 – 800 = 400
Como foram 8 pessoas, temos:
400 ÷ 8 = 50
R$ 50,00 por convidado
Resolução em vídeo no Tiktok: clique aqui
Questão 9
Q75F (UEMA) O proprietário de uma oficina mecânica presta serviços de manutenção e de recuperação de carros de passeio, além de troca e de reposição de óleos em geral. Ao analisar por um ano a troca regular de óleo do motor em 45 carros de passeio de seus clientes com fidelidade, verificou que ela é efetuada em um período médio de quatro meses e que são utilizados 3 litros de óleo em cada troca.
Com base nessas informações, pode–se concluir que o consumo de litros de óleo nos carros de passeio dessa oficina dos clientes com fidelidade, em um semestre, é igual a:
a) 250,0
b) 225,0
c) 222,5
d) 205,0
e) 202,5
Resposta
Em 4 meses os 45 carros consumiram
45.3 = 135 litros de óleo.
Em 2 meses, os carros consumiram
135÷2 = 67,5 litros óleo.
Letra E
Questão 10
Q77F (UEMA) Uma lanchonete investiu R\$ 2.800,00 na compra de equipamentos e, com as demais despesas na produção, gasta R\$ 1,75 por lanche produzido. Se cada lanche é vendido por R\$ 3,45,qual o número mínimo de lanches que essa lanchonete deve vender para obter um lucro maior que R\$ 3.219,00?
Resposta
O lucro para um lanche vendido será
3,45 – 1,75 = 1,7.
Assim, para ter um lucro maior que 3219, faremos:
$\begin{array}{c}
\frac{{2800 + 3219}}{1,7} = \frac{{6019}}{{1,7}} ≅ 3540,59
\end{array}$
Assim, ela precisa vender 3541 lanches.
Questão 11
Q78F (UEMA) Um determinado paciente internado num grande hospital de São Luís está necessitando receber 500 ml de soro adicionado de 25 mL de analgésico. Sabe–se que 1 mL corresponde a 20 gotas e que devem ser administradas 35 gotas por minuto (taxa de infusão).
Quanto tempo paciente levará para receber toda medicação sem a interrupção do cotejamento?
a) 6 horas e 25 minutos.
b) 37 horas e 30 minutos.
c) 6 horas e 17 minutos.
d) 6 horas e 15 minutos.
e) 5 horas e 57 minutos.
Resposta
O total é 500 mL + 25 mL = 525 mL
Em gotas, teremos 525.20 = 10500 gotas.
Considerando a taxa de infusão, o tempo será:
$\begin{array}{c}
\frac{{10500}}{35} = 300’\end{array}$
Totalizando 5 horas
Assim, a questão deve ser anulada.
Questão 12
Q86F (UEMA) Para participar do torneio Copa Norte de Natação, na cidade de Belém do Pará, nos dias 18,19 e 20 deabril de 2013, uma equipe do Maranhão analisou duas propostas de viagens, apresentadas no quadro a seguir com seus respectivos hotéis:
| AVIÃO | Valor total R\$ 4 200,00 (ida e volta) Hotel A – diária R\$ 125,00 por pessoa |
| ÔNIBUS FRETE | Valor total R\$ 4 500,00 (ida e volta) Hotel B – diária R\$ 115,00 por pessoa |
Considere que o valor total de cada plano será dividido igualmente entre os vinte participantes desta equipe e que foi escolhido o plano mais barato. Nessas condições, o preço pago por Dona Maria e seus dois filhos, em passagens e em diárias nos dias considerados, em reais, foi de:
a) 1775.
b) 1710.
c) 1500.
d) 1380.
e) 1365.
Resposta
Avião/Hotel A
4200 + 3.20.125 = 11700
11700 : 20 = 585
Ônibus–Frete/Hotel B
4500 + 3.20.115 = 11400
11400 : 20 = 570
O mais vantajoso é a viagem de ônibus, resultando em um custo para Dona Maria de:
3.570 = 1710
Letra B
Questão 13
Q89F (UEMA) Em um parque ecológico da cidade de Floresta Negra, o ingresso para visitação custa R$ 5,00 e crianças menores de 10 anos não pagam. Em um domingo, cerca de 2.550 pessoas visitaram esse parque, e as bilheterias arrecadaram a importância de R\$ 5.500,00. Calcule o número de crianças com menos de 10 anos que visitaram o parque nesse dia.
Resposta
Encontrando o número de pagantes:
5500/5 = 1100 pagantes, ou seja, 1100 maiores de 10 anos.
Sendo o total de pessoas 2550, o número de crianças menores de 10 anos será
2550 – 1100 = 1450
Para mais questões da UEMA por assunto clique aqui

