[latexpage] Fique com a prova resolvida do Colun 2020 1° ano. Em cada questão temos as respostas comentadas do Colun.
Visite a página com tudo sobre este seletivo do COLUN: clique aqui
📺 Esta prova está resolvida em vídeo: clique aqui
Questão 16
Q1584F (COLUN UFMA) André gastou a quarta parte do seu 1º salário com moradia e a terça parte com água, luz e alimentação. Sobraram, ainda, RS 400,00. Qual foi o valor que André recebeu no seu 1º salário?
a) RS 320,00
b) RS 960,00
c) RS 1.040,00
d) RS 560,00
e) RS 940,00
Resposta
Faremos o valor do pagamento igual a x.
Os gastos somam $\color{red}\frac{1}{4} + \frac{1}{3} = \frac{{3 + 4}}{{12}} = \frac{7}{{12}}$
Em fração, sobram $\color{red}\frac{5}{{12}}$. Em valores do pagamento x, isso equivale a 400. Logo:
$\color{red}\frac{5}{{12}} \cdot x = 400 \Rightarrow x = \frac{{400 \cdot 12}}{5} = 960$
Letra B
Questão 17
Q1585F (COLUN UFMA) Dados dois números naturais, a soma dos quadrados desses números é igual a 520. Dividindo-se o maior deles pelo menor, obtém-se 3 como quociente e 4 de resto. Qual o produto desses dois números naturais?
a) 50,4
b) 5184
c) 132
d) 144
e) 28
Resposta
Chamaremos os números de x e y.
Pela primeira sentença, temos: x² + y² = 520. Já pela segunda:
| x | y |
| 4 | 3 |
Pela prova real: 3y + 4 = x
Substituindo na primeira equação:
x² + y² = 520 ⟹ (3y + 4)² + y² = 520 ⟹ 9y² + 24y + 16 + y² = 520
10y² + 24y – 504 = 0 ⟹ 5y² + 12y – 252 = 0
Encontrando o delta:
∆ = b² – 4ac = 12² – 4.5.(-252) = 144 + 20.252 = 5184
Usando a fórmula:
$\color{red}y = \frac{{ – b \pm \sqrt \Delta }}{{2a}} \Rightarrow y = \frac{{ – 12 \pm \sqrt {5184} }}{{10}} = \frac{{ – 12 \pm 72}}{{10}}$
$\color{red}{y_1} = \frac{{ – 12 + 72}}{{10}} = \frac{{60}}{{10}} = 6$
$\color{red}{y_2} = \frac{{ – 12 – 72}}{{10}}$ (não convém, já que não é natural)
Vamos encontrar o y em:
3y + 4 = x ⟹ 3.6 + 4 = x ⟹ x = 22
O produto xy = 22.6 = 132
Letra C
Questão 18
Q1586F (COLUN UFMA) A placa de propaganda de uma loja de confecções tem a forma de um trapézio. Sua área é de 11,16 𝑚² e as medidas de suas bases são 4 𝑚 e 3,20 𝑚. Qual é a medida da altura da placa?
a) 6,4 m
b) 7,2 m
c) 3,6 m
d) 3,1 m
e) 6,2 m
Resposta
A área do trapézio é dada por $\color{red}A = \frac{{\left( {B + b} \right) \cdot h}}{2}$. Daí, teremos:
$\color{red} 11,16 = \frac{{\left( {4 + 3,2} \right) \cdot h}}{2} \Rightarrow 22,32 = 7,2 \cdot h \Rightarrow h = 3,1$
Letra D
Questão 19
Q1587F (COLUN UFMA) Qual a função que representa o valor de y a ser pago por Giovana, após ela receber um desconto de 4% sobre o valor de x numa compra?
a) 𝑦 = 1,04𝑥
b) 𝑦 = 𝑥−4
c) 𝑦 = 1,4𝑥
d) 𝑦 = −4𝑥
e) 𝑦 = 0,96𝑥
Resposta
O valor y será:
$\color{red}y = x – \frac{4}{{100}} \cdot x \Rightarrow y = x – 0,04x \Rightarrow y = 0,96x$
Letra E
Questão 20
Q1588F (COLUN UFMA) Os lados congruentes de um triângulo isósceles medem 10 cm cada um e a base mede 6 cm. Qual é, aproximadamente, a área da região triangular limitada por esse triângulo? Considere para as extrações de raízes apenas um algarismo após a vírgula.
a) 9,5 cm²
b) 28,5 cm²
c) 45 cm²
d) 60 cm²
e) 91 cm²
Resposta
Ilustrando a situação
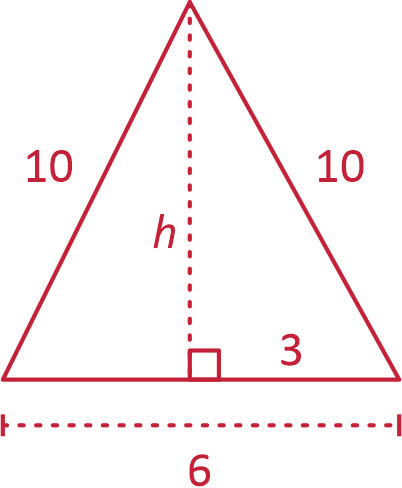
Aplicando o Teorema de Pitágoras:
$\color{red}{h^2} + {3^2} = {10^2} \Rightarrow {h^2} = 91 \Rightarrow h = \sqrt {91} $
Note que 9,5.9,5 = 90,25, então h ≅ 9,5.
A área do triângulo será: $\color{red}\frac{{6 \cdot 9,5}}{2} = 3 \cdot 9,5 = {\rm{28}}{\rm{,5}}$
Letra B
Questão 21
Q1589F (COLUN UFMA) A razão entre as medidas da base e da altura de um retângulo é igual a , e o valor do perímetro desse retângulo é de 30 𝑐𝑚. Qual a área da região desse retângulo?
a) 9 cm²
b) 27 cm²
c) 54 cm²
d) 18 cm²
e) 81 cm²
Resposta
Usando a proporcionalidade dada:
$\color{red}\frac{b}{h} = \frac{2}{3} \Rightarrow b = \frac{{2h}}{3}$
Como o perímetro é 30, teremos:
2b + 2h = 30 ⟹ b + h = 15
Substituindo o valor de b:
$\color{red}\frac{{2h}}{3} + h = 15 \Rightarrow 2h + 3h = 45 \Rightarrow h = 9$
Com b + h = 15, temos b = 15 – 9 = 6.
A área da região será 6.9 = 54 cm²
Letra C
Questão 22
Q1590F (COLUN UFMA) O reservatório de água da casa da avó de Israele tem a forma de um cilindro. Usando um barbante, Israele contornou a base do reservatório e constatou que a circunferência tem 15,5m. Qual o valor aproximado do raio da base desse reservatório? (Use 𝜋 = 3,1)
a) 3,14 m
b) 5 m
c) 6,2 m
d) 2,5 m
e) 6,5 m
Resposta
C = 2πr ⟹ 15,5 = 2.3,1.r ⟹ 15,5 = 6,2r ⟹ r = 2,5
Letra D
Questão 23
Q1564F (COLUN UFMA) A divisória entre a sala e a copa de uma casa tem 7,0 metros de comprimento por 3,0 metros de altura. Nessa parede há uma porta de 1,8 metros de largura por 2,1 metros de altura.

Se retirarmos a área da porta da área da divisória, podemos afirmar que a área somente de parede é:
a) 17,22 m²
b) 21,0 m²
c) 3,78 m²
d) 24,78 m²
e) 6,3 m²
Resposta
A área da parede é 3.7 = 21m²
A área da porta é 2,1.1,8 = 3,78m²
Fazendo a subtração pedida 21 – 3,78 = 17,22 m²
Letra A
Questão 24
INGLÊS
Q1591F (COLUN UFMA) O Parque Estadual do Sítio do Rangedor é uma unidade de conservação brasileira localizada na cidade de São Luís, no Maranhão, com aproximadamente 120 hectares de área.
Sabendo que cada hectare corresponde a uma área quadrada de lado igual a 100 metros. O valor da área desse parque, em metros quadrados, é:
a) 120.000 m²
b) 10.000 m²
c) 1.200.000 m²
d) 100.000 m²
e) 12.000 m²
Resposta
1 ha = 100.100 = 10 000 m².
120 ha = 120 . 10 000 = 1 200 000 m²
Letra C
Questão 25
Q1592F (COLUN UFMA) Uma loja de São Luís, apresentou a promoção conforme imagem a seguir.

Sabendo que Sr. Hugo comprou no dia da promoção uma geladeira, um fogão e uma máquina de lavar roupas pelos valores, sem desconto, de RS 2.700,00, RS 1.800,00 e RS 1.600,00, respectivamente. Então o valor, com desconto, efetivamente pago pela compra foi:
a) RS 1.620,00
b) RS 6.100,00
c) RS 2.430,00
d) RS 5.490,00
e) RS 1.440,00
Resposta
O total é 2 700 + 1 800 + 1600 = 6 100.
Fazendo o desconto de 10%
$\color{red}6100 – \frac{{10}}{{100}} \cdot 6100 = 6100 – 610 = 5490$
Letra D
Questão 26
Q1593F (COLUN UFMA) O gráfico e a tabela a seguir, representam uma função polinomial do primeiro grau.
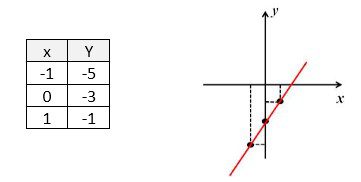
A função que melhor representa a reta é:
a) 𝑦 = 2𝑥 − 3
b) 𝑦 = 𝑥 − 3
c) 𝑦 = 2𝑥
d) 𝑦 = 2𝑥 − 2
e) 𝑦 = 𝑥 − 2
Resposta
Uma função afim é sempre do tipo y = ax + b
O b é onde o gráfico “corta” o eixo y. E isso acontece no ponto (0, -3), ou seja, b = -3.
Temos até aqui a função y = ax – 3.
Agora, para descobrirmos o a, vamos usar o ponto (1, – 1):
y = ax – 3 ⟹ -1 = a.1 – 3 ⟹ 2 = a
A função procurada é y = 2x – 3
Letra A
Questão 27
Q1594F (COLUN UFMA) A figura ABC tem seus vértices na circunferência de centro em O. O ângulo com vértice em A tem a medida igual a X.
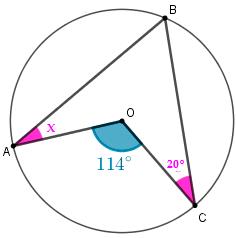
Considerando que um ângulo inscrito é metade do ângulo central marcado sobre o mesmo arco, podemos afirmar sobre o ângulo X.
a) que o ângulo X é 33°
b) que o ângulo X é 37°
c) que o ângulo X é 46°
d) que também é 20°
e) que o ângulo X + 20° = 180°
Resposta
Vamos prolongar o raio AO determinando um arco com medida 2x e o mesmo faremos com OC, determinando um arco de 40°.
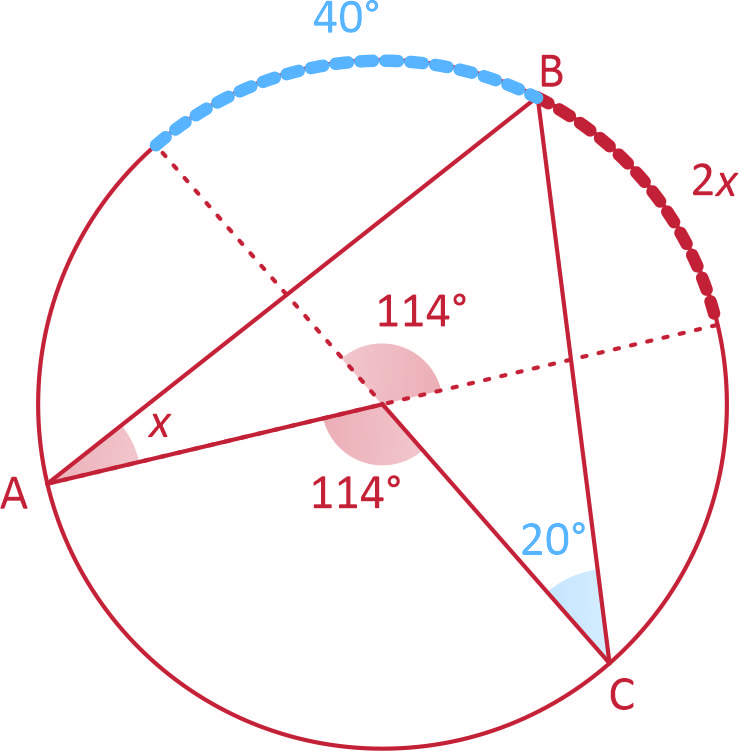
Como o 114° é central, teremos:
114° = 40 + 2x
114 – 40 = 2x
74 = 2x
x = 37
Letra B
Questão 28
Q1595F (COLUN UFMA) Considerando uma equação do segundo grau na forma 𝑥²+𝑏𝑥+𝑐=0 e sabendo que suas raízes 𝑥1 e 𝑥2 tem valor 1 e 4, respectivamente, determine a equação que representa uma equação do segundo grau com essas soluções e assinale a opção correspondente.
a) x² − 4𝑥 + 5 = 0
b) x² − 6𝑥 + 4 = 0
c) x² − 4𝑥 + 1 = 0
d) x² − 𝑥 + 4 = 0
e) x² − 5𝑥 + 4 = 0
Resposta
Usaremos soma e produto das raízes
S = 1 + 4 = 5
P = 1.4 = 4
Em x² – Sx + P = 0, teremos:
x² – 5x + 4 = 0
Letra E
Questão 29
Q1596F (COLUN UFMA) Temos uma pirâmide com sombra igual a 60 metros e um mourão (estaca fincada perpendicular ao solo) com medidas indicadas na figura.
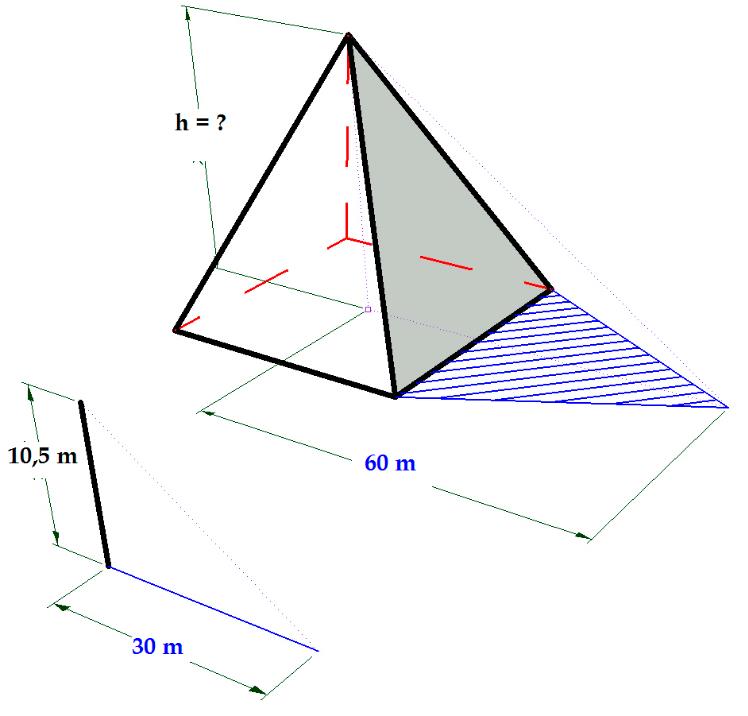
Calculando a altura da pirâmide (h) obteremos
a) 10,5 metros
b) 42 metros
c) 21 metros
d) 1.800 metros
e) 600,50 metros
Resposta
Aplicando razões de semelhança, teremos:
$\color{red}\frac{h}{{10,5}} = \frac{{60}}{{30}} \Rightarrow \frac{h}{{10,5}} = 2 \Rightarrow h = 21$
Letra C
Questão 30
Q1597F (COLUN UFMA) Dentre as alternativas a seguir, a que melhor define o conceito de polígono é:
a) Uma figura aberta, formada por segmentos de retas e arcos de circunferência.
b) Uma figura aberta, formada apenas por segmentos de retas.
c) Uma figura fechada, limitada por segmentos de retas podendo ter arcos de circunferência.
d) Uma figura fechada, limitada por segmentos de retas.
e) Qualquer figura aberta ou fechada, formada apenas por segmentos de retas.
Resposta
Letra D