[latexpage]
Fique com a prova resolvida da UEMA 2019. Em cada questão temos a resposta comentada.
Questão 45 – 1ª Etapa
Corridas de 50 m, geralmente, são provas de aptidão física (concursos da Polícia, Guarda Civil, etc.), na qual o candidato deverá correr 50 m em um tempo mínimo. Quanto menor o tempo, melhor será sua classificação. Num Concurso Público para Guarda Municipal, um determinado candidato realizou o Teste de Aptidão Física, percorrendo o espaço e o tempo, de acordo com o gráfico representado a seguir.
Analise o gráfico que mostra o desempenho do candidato. Para tanto, considere S, em metros, e t, em segundos.
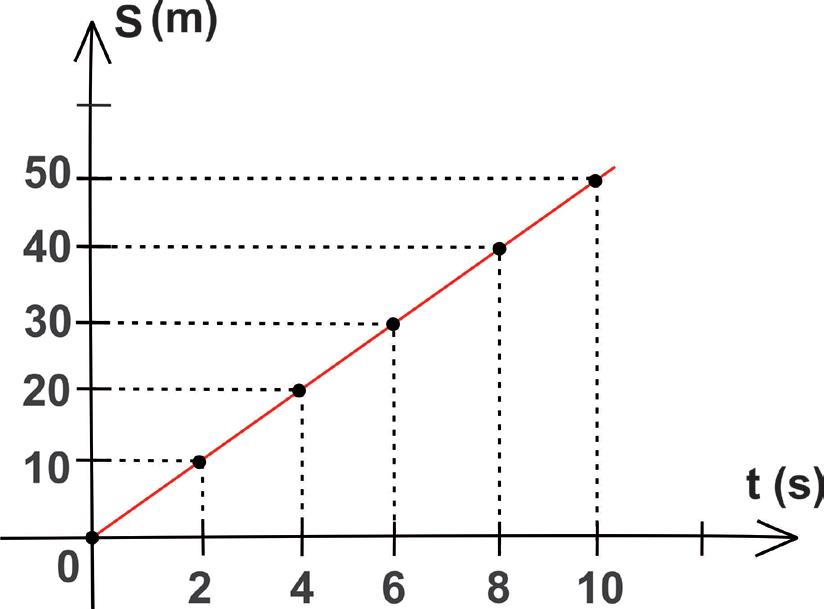
De acordo com o gráfico de desempenho do candidato, a função horária correspondente é igual
a) S = –5t
b) S = –4t
c) S = 4t
d) S = 3t
e) S = 5t
Resposta
Sendo o gráfico a representação de uma reta, na forma f(x) = ax + b, com f(x) = S e x = t, teremos:
Em S = ax + b no ponto (2,10)
10 = 2a + b
Em S = ax + b no ponto (4,20)
20 = 4a + b
Juntando em um sistema:
$latex \color{red}\left\{ \begin{array}{c}10=2a+b\\20=4a+b\end{array} \right.$
$latex \color{red}20-10=4a-2a+b-b\Rightarrow a=5\therefore b=0$
f(x) = ax + b ⟹ f(x) = 5x + 0⟹ S = 5t
Letra E
Questão 47 – 1ª Etapa
O proprietário de um veículo cujo tanque de combustível de capacidade para 60 litros, ao passar por um posto de combustível, vê a placa a seguir.

O atento proprietário verifica que o carro está apenas com ¼ do tanque com gasolina. Ele gastará para completar o tanque com gasolina, a seguinte quantia:
a) RS 61,35
b) RS 184,05
c) RS 245,40
d) RS 229,04
e) RS 244,38
Resposta
O tanque possuía 15 litros, como vemos em:
$latex \color{red}\frac{1}{4}.60=15$
Para completar, ele precisa de 45 litros, que equivalem a 45.4,09 = RS 184,05
Letra B
Questão 48 – 1ª Etapa
A cada cinco brasileiros, um está obeso. Mais da metade da população está acima do peso. IMC é o índice internacional mais usado para definir se uma pessoa está abaixo do peso, no peso ideal ou acima dele. O cálculo do IMC é feito dividindo o peso, em quilogramas, pela altura (dada em metros) ao quadrado, quanto maior o IMC, maior grau de obesidade e maior risco de doenças como diabetes, AVC, infarto, pressão alta, trombose, entre outras.
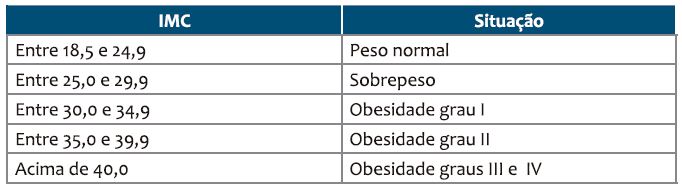
Uma pessoa com 67 kg e 1,60 metros de altura apresenta, de acordo com o quadro, a situação de
a) Obesidade grau II
b) Obesidade grau III e IV
c) Sobrepeso
d) Obesidade grau 1
e) Peso normal
Resposta
$latex \color{red}IMC=\frac{{67}}{{{{{\left( {1,6} \right)}}^{2}}}}=\frac{{67}}{{2,56}}\cong 26,18$
Letra C
Questão 49 – 1ª Etapa
Áreas como microbiologia e biologia molecular utilizam com muita frequência a técnica conhecida como “cultura bacteriana”. A referida técnica consiste basicamente em promover o crescimento populacional de uma colônia bacteriana in vitro. Analise a seguinte situação:
Em laboratório da UEMA, sob condições específicas com acompanhamento rigoroso do crescimento populacional de uma colônia de bactérias, foi observado que esse crescimento estava descrito pela função $latex N=300\,x\,{{2}^{t}}$ , onde t representa o tempo em dias e N é o número de bactérias total da colônia num dado tempo.
Considere a função descrita no laboratório da UEMA. Indique em quantos dias a população de bactérias será igual a 76800 bactérias nessa colônia.
a) 8
b) 7
c) 25, 6
d) 12,8
e) 128
Resposta
$latex \color{red}\begin{array}{c}76800=300\,x\,{{2}^{t}}\Rightarrow \frac{{76800}}{{300}}={{2}^{t}}\Rightarrow 256={{2}^{t}}\\{{2}^{8}}={{2}^{t}}\Rightarrow t=8\end{array}$
Letra A
Questão 50 – 1ª Etapa
Um determinado paciente internado num grande hospital de São Luís está necessitando receber 500 ml de soro adicionado de 25 mL de analgésico. Sabe–se que 1 mL corresponde a 20 gotas e que devem ser administradas 35 gotas por minuto (taxa de infusão).
Quanto tempo paciente levará para receber toda medicação sem a interrupção do cotejamento?
a) 6 horas e 25 minutos.
b) 37 horas e 30 minutos.
c) 6 horas e 17 minutos.
d) 6 horas e 15 minutos.
e) 5 horas em 57 minutos.
Para mais conteúdo sobre a UEMA, clique aqui.
Resposta
O total é 500 mL + 25 mL = 525 mL. Em gotas, teremos 525.20 = 10500 gotas. Considerando a taxa de infusão, o tempo será:
$latex \color{red}\frac{{10500}}{{35}}=300’$
Ou seja, 300 minutos. Totalizando 5 horas.
Assim, a questão deve ser anulada.
Para mais conteúdo sobre a UEMA, clique aqui.
Questão 01 – 2ª Etapa – Prova resolvida UEMA 2019
Dona Maria da Graça queria trocar o revestimento do piso de sua casa de 72 m². Ao fazer o orçamento, encontrou as seguintes informações:
| Tipo | Dimensão da lajota (cm x cm) | Quantidade de lajotas por caixa | Preço por caixa (RS) |
| I | 30×30 | 20 | 42,00 |
Calcule o valor que Dona Maria da Graça gastará para revestir sua casa.
Resposta
Cada lajota ocupa 30×30 = 900 cm² = 0,09 m²
Agora, vamos descobrir a quantidade total de lajotas:
$latex \color{red}\displaystyle \frac{{72{{m}^{2}}}}{{0,09{{m}^{2}}}}=\frac{{72}}{{9/100}}=\frac{{72}}{9}.100=800$
O valor total será:
$latex \color{red}\frac{{800}}{{20}}.42=\text{1680}$
Questão 02 – 2ª Etapa
No regulamento do campeonato brasileiro de futebol da série C de 2018, nos artigos 11 e 12, lê–se:
Na primeira fase os 20 (vinte) clubes constituirão os grupos A e B com 10 (dez) clubes cada, dentro de cada grupo todos os clubes jogarão entre si, em turno (ida) e returno (volta).
Calcule a quantidade de jogos do turno (ida) que foram realizados no grupo A.
Resposta
$latex \color{red}{{C}_{{10,2}}}=\frac{{10!}}{{2!\left( {10-2} \right)!}}=\frac{{10.9.8!}}{{2!8!}}=\frac{{10.9}}{2}=45$
Questão 03 – 2ª Etapa
Quando viajamos pelo país em rodovias administradas por concessionárias, é comum vermos telefones de segurança instalados no acostamento das rodovias. A concessionária RodaBEM ganhou uma licitação para administrar um trecho de uma determinada rodovia e observou que já havia dois telefones de segurança instalados no acostamento do trecho: um, no km 2; outro, no km 86.
Decidiu–se colocar entre os dois telefones, já instalados, outros 13 telefones de segurança, mantendo exatamente a mesma distância entre dois telefones consecutivos.
Calcule a distância, em km, a ser respeitada entre dois telefones consecutivos.
Resposta
Considerando como o primeiro termo sendo 2, o último termo sendo 86 e número de termos sendo 15, já que serão adicionados mais treze termos. Teremos:
$ \color{red}{a_n} = {a_1} + \left( {n – 1} \right)r \Rightarrow \\86 = 2 + \left( {15 – 1} \right) \cdot r \Rightarrow \frac{{84}}{{14}} = r = 6$
Questão 04 – 2ª Etapa
Durante a copa do mundo de futebol da Rússia, por diversas vezes, as redes televisivas mostraram a trajetória feita pela bola durante o chute. Suponha as seguintes condições: que um jogador esteja a uma distância de 40 metros de seu companheiro de time, e exatamente, no meio deles, há um jogador do time adversário; a bola estava a 4 metros acima do chão quando passou pelo jogador adversário.
Essas condições estão ilustradas na figura a seguir:
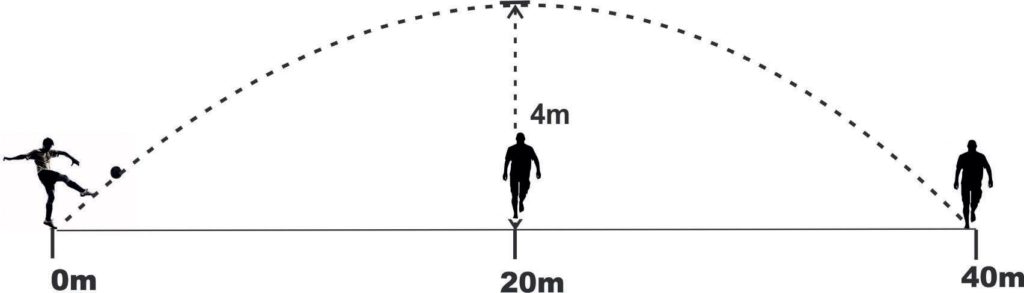
Determine a equação da parábola que descreve a trajetória dessa bola.
Resposta
A trajetória da bola é uma Parábola:
$latex \color{red} f\left( x \right)=a{{x}^{2}}+bx+c$
Na imagem acima, vemos claramente os pontos (x,y), (0,0), (20,4) e (40,0).
Assim, temos logo que o valor de c = 0. Usando os pontos (20,4) e (40,0):
$latex \color{red}\displaystyle \left\{ \begin{array}{l}4=a{{.20}^{2}}+b.20\\0=a{{.40}^{2}}+b.40\end{array} \right.\Rightarrow \left{ \begin{array}{l}4=400a+20b\left( {x4} \right)\\0=1600a+40b\end{array} \right. \Rightarrow $
$latex \color{red}\displaystyle \left\{ \begin{array}{l}16=1600a+80b\\0=1600a+40b\end{array} \right.\downarrow -$
$latex \color{red}\displaystyle 16=40b\Rightarrow b=\frac{{{{{16}}^{{:8}}}}}{{{{{40}}_{{:8}}}}}=\frac{2}{5}$
$latex \color{red}\displaystyle 0=1600a+40.\frac{2}{5}\Rightarrow -1600a=16\Rightarrow a=\frac{{-1}}{{100}}$
$latex \color{red}f\left( x \right)=a{{x}^{2}}+bx+c\Rightarrow f\left( x \right)=\frac{{-{{x}^{2}}}}{{100}}+\frac{{2x}}{5}+0$
Questão 05 – 2ª Etapa
Qualquer quantidade de água exposta sofrerá a evaporação, pois este é um processo natural físico. Com uma piscina não seria diferente: incidência constante de sol, de calor, de vento e de baixa umidade contribui para o nível da água abaixar diariamente.
Entretanto, por experiências, se diz que há um limite máximo de aproximadamente 5 cm / semana ou 3 mm / dia de evaporação, que, obviamente, varia de acordo com o tamanho da superfície da piscina e de fatores meteorológicos, como os citados acima. Provavelmente, quando esses valores são ultrapassados, a piscina apresenta problemas de vazamento. Tendo como foco uma piscina semiolímpica, de base retangular, com 25 m de comprimento, 20 m de largura e uma profundidade uniforme de 1,3 m (da lâmina d’água até o fundo da piscina), pergunta-se:
a) Considerando o limite de 5 cm por semana de evaporação, calcule a quantidade de litros de água que restará na piscina, após uma semana sem reposição alguma de água.
b) Considerando a evaporação de 3 mm por dia, calcule quantos litros de água deverão ser recolocados na piscina, após 12 dias, para que a piscina retorne ao nível de água inicial.
Resposta
a) Volume da Piscina:
V = 25.20.1,3 = 650m³ = 650000 dm³ = 650000 L
A evaporação corresponde: E = 25.20.0,05 = 25m³.
1m³ = 1000L
25m³ = 25000 L
Restam na piscina: 650000 – 25000 = 625000
b) A evaporação corresponde:
25.20.12.0,003 = 18m³ = 18000 dm³ = 18000 L
Questão 06 – 2ª Etapa
Uma pista de atletismo será construída na cidade ABC em torno de um terreno formado por um retângulo (campo de futebol) com 100 metros de comprimento e 72 metros de largura e duas semicircunferências cujo diâmetro coincide com a largura da área retangular. Observe a figura a seguir:
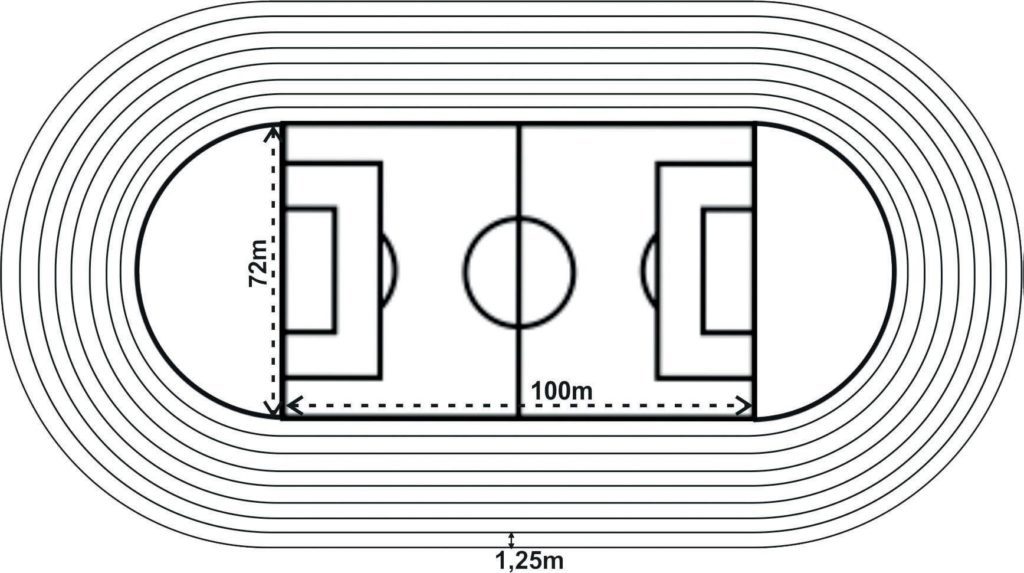
O prefeito da cidade ABC deseja revestir essa pista de atletismo, e a empreiteira que ganhou a licitação cobrará RS 120, 00 por metro quadrado aplicado de revestimento. A pista terá 8 raias (são os caminhos pelos quais os atletas devem correr) de 1,25 metros de largura cada uma.
Calcule o preço total gasto para revestir toda essa pista. Considere π = 3,14.
Resposta
A largura total da pista será 8.1,25 = 10m.
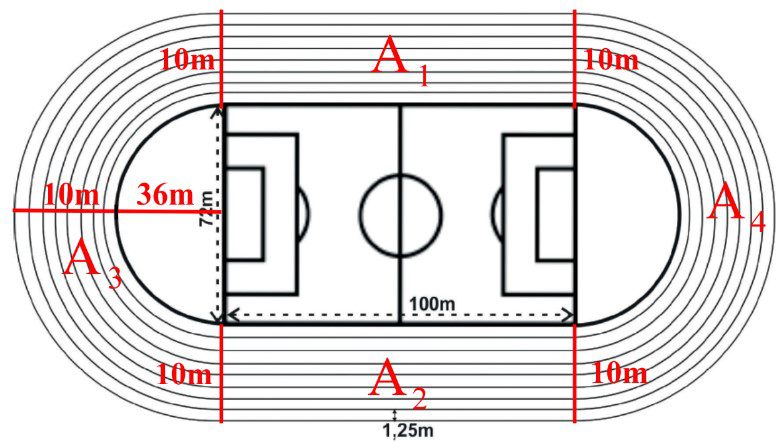

Somando: ![]()
Gasto: 4574,8.120 = RS 548 976,00
Para mais conteúdo sobre a UEMA, clique aqui.