Fique com as Questões de Analise Combinatória no ENEM. Em cada questão temos a resposta comentada.
Questão 1
Q733M (ENEM) Um prédio, com 9 andares e 8 apartamentos de 2 quartos por andar, está com todos os seus apartamentos à venda. Os apartamentos são identificados por números formados por dois algarismos, sendo que a dezena indica o andar onde se encontra o apartamento, e a unidade, um algarismo de 1 a 8, que diferencia os apartamentos de um mesmo andar. Quanto à incidência de sol nos quartos desses apartamentos, constatam-se as seguintes características, em função de seus números de identificação:
• naqueles que finalizam em 1 ou 2, ambos os quartos recebem sol apenas na parte da manhã;
• naqueles que finalizam em 3, 4, 5 ou 6, apenas um dos quartos recebe sol na parte da manhã;
• naqueles que finalizam em 7 ou 8, ambos os quartos recebem sol apenas na parte da tarde.
Uma pessoa pretende comprar 2 desses apartamentos em um mesmo andar, mas quer que, em ambos, pelo menos um dos quartos receba sol na parte da manhã.
De quantas maneiras diferentes essa pessoa poderá escolher 2 desses apartamentos para compra nas condições desejadas?
a) $9 \cdot \frac{6!}{(6-2)!}$
b) $9 \cdot \frac{6!}{(6-2)! \cdot 2!}$
c) $9 \cdot \frac{4!}{(4-2)! \cdot 2!}$
d) $9 \cdot \frac{2!}{(2-2)! \cdot 2!}$
e) $9 \cdot \left( \begin{array}{cl} \frac{8!}{(8-2)! \cdot 2!} -1 \end{array}\right)$
Resposta
Os apartamentos que possuem pelo menos um dos quartos receba sol na parte da manhã são os terminados em 1,2,3,4,5,6 (6 opções)
Como essa pessoa quer comprar 2, temos que fazer combinação:
$C_{6,2} =\frac{6!}{2!(6-2)!}$ para a escolha somente em um andar.
Como o prédio é composto por 9 andares:
$9 \cdot \frac{6!}{(6-2)! \cdot 2!}$
Letra B
Resolução em vídeo clique aqui
Questão 2
Q751M (ENEM) Uma montadora de automóveis divulgou que oferta a seus clientes mais de 1000 configurações diferentes de carro, variando o modelo, a motorização, os opcionais e a cor do veículo. Atualmente, ela oferece 7 modelos de carros com 2 tipos de motores: 1.0 e 1.6. Já em relação aos opcionais, existem 3 escolhas possíveis: central multimídia, rodas de liga leve e bancos de couro, podendo o cliente optar por incluir um, dois, três ou nenhum dos opcionais disponíveis.
A) 8.
B) 9.
C) 11.
D) 18.
E) 24.
Resposta
Organizando os dados, temos: 7 modelos, 2 motores.
Cada configuração de opcionais corresponde a um subconjunto do conjunto {central multimídia, rodas de liga leve, bancos de couro} menos o subconjunto vazio, ou seja, 3² – 1 = 8.
Para as cores temos x. Para temos mais de 1 000 configurações, faremos
7.2.8.x > 1000
7x > 62,5
x > 8,93
Portanto, a quantidade mínima de cores que a montadora deverá disponibilizar é 9.
Letra B
Questão 3
Q745M (ENEM) Em um jogo de bingo, as cartelas contêm 16 quadrículas dispostas em linhas e colunas. Cada quadrícula tem impresso um número, dentre os inteiros de 1 a 50, sem repetição de número. Na primeira rodada, um número é sorteado, aleatoriamente, dentre os 50 possíveis. Em todas as rodadas, o número sorteado é descartado e não participa dos sorteios das rodadas seguintes. Caso o jogador tenha em sua cartela o número sorteado, ele o assinala na cartela. Ganha o jogador que primeiro conseguir preencher quatro quadrículas que formam uma linha, uma coluna ou uma diagonal, conforme os tipos de situações ilustradas na Figura 1.
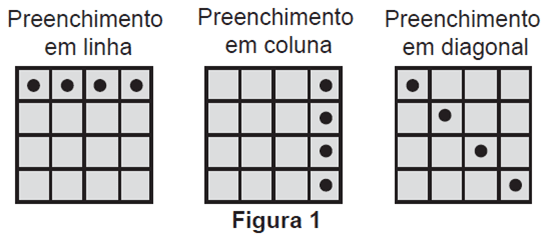
O jogo inicia e, nas quatro primeiras rodadas, foram sorteados os seguintes números: 03, 27, 07 e 48. Ao final da quarta rodada, somente Pedro possuía uma cartela que continha esses quatro números sorteados, sendo que todos os demais jogadores conseguiram assinalar, no máximo, um desses números em suas cartelas. Observe na Figura 2 o cartão de Pedro após as quatro primeiras rodadas.
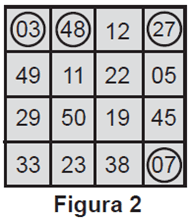
A probabilidade de Pedro ganhar o jogo em uma das duas próximas rodadas é:
a) $\frac{1}{46} +\frac{1}{45}$
b) $\frac{1}{46} +\frac{2}{46 \cdot 45}$
c) $\frac{1}{46} +\frac{8}{46 \cdot 45}$
d) $\frac{1}{46} +\frac{43}{46 \cdot 45}$
e) $\frac{1}{46} +\frac{49}{46 \cdot 45}$
Resposta
Temos um total de 50 número. Na figura 2 vemos que já foram sorteados 4, daí nosso universo possível agora são 50 – 4 = 46.
1° caso: ganhar acertando o número 12 na primeira tentativa e formar a linha:
$\frac{1}{46}$
2° caso: não sair o 12 na primeira e sair somente na segunda e formar a linha:
$\frac{45}{46} \cdot \frac{1}{45}= \frac{45}{46 \cdot 45}$
3° caso: sair 5 na primeira e 45 na segunda e formar a coluna. Note que o contrário também é válido, logo faremos o resultado dobrado:
$\frac{1}{46} \cdot \frac{1}{45} \cdot 2= \frac{2}{46 \cdot 45}$
4° caso: sair 11 na primeira e 19 na segunda e formar a diagonal. Note que o contrário também é válido, logo faremos o resultado dobrado:
$\frac{1}{46} \cdot \frac{1}{45} \cdot 2= \frac{2}{46 \cdot 45}$
Somando as probabilidades:
$\frac{1}{46} + \frac{45}{46 \cdot 45} + \frac{2}{46 \cdot 45} + \frac{2}{46 \cdot 45}= \frac{1}{46}+ \frac{49}{46 \cdot 45}$
Letra E
Questão 4
Q749M (ENEM) A World Series é a decisão do campeonato norte-americano de beisebol. Os dois times que chegam a essa fase jogam, entre si, até sete partidas. O primeiro desses times que completar quatro vitórias é declarado campeão.
Considere que, em todas as partidas, a probabilidade de qualquer um dos dois times vencer é sempre .
Qual é a probabilidade de o time campeão ser aquele que venceu a primeira partida da World Series?
a) $\frac{35}{64}$
b)$\frac{40}{64}$
c) $\frac{42}{64}$
d) $\frac{44}{64}$
e) $\frac{52}{64}$
Resposta
Sejam A e B os times que chegaram à World Series e considere que o time A venceu a primeira partida. A equipe A pode ser campeã nos seguintes cenários:
a) ganhando os jogos 2, 3 e 4:
| Jogo | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Vencedor | A | A | A | A | |||
| Probabilidade | 1 | $\frac{1}{2}$ | $\frac{1}{2}$ | $\frac{1}{2}$ |
Esse cenário acontece com probabilidade: $1 \cdot \frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{2}= \frac{1}{8}$
b) perdendo um e ganhando dois dos jogos de 2 a 4, e ganhando o jogo 5. Um exemplo em que isso acontece é:
| Jogo | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Vencedor | A | A | A | A | A | ||
| Probabilidade | 1 | $\frac{1}{2}$ | $\frac{1}{2}$ | $\frac{1}{2}$ | $\frac{1}{2}$ |
Considerando que os resultados dos jogos 2 a 4 podem ocorrer em qualquer ordem, o número de maneiras como esse cenário pode ocorrer é o número de permutações de BAA, ou $\frac{3!}{2!}$.
Esse cenário acontece com probabilidade: 1 \cdot \frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{2} \cdot \frac{3!}{2!}= \frac{3}{16}
c) perdendo dois e ganhando dois dos jogos de 2 a 5, e ganhando o jogo 6. Um exemplo em que isso acontece é:
| Jogo | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Vencedor | A | A | A | A | A | A | |
| Probabilidade | 1 | $\frac{1}{2}$ | $\frac{1}{2}$ | $\frac{1}{2}$ | $\frac{1}{2}$ | $\frac{1}{2}$ |
Considerando que os resultados dos jogos 2 a 5 podem ocorrer em qualquer ordem, o número de maneiras como esse cenário pode ocorrer é o número de permutações de BBAA, ou $\frac{4!}{2!2!}$ .
Esse cenário acontece com probabilidade: $1 \cdot \frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{2} \cdot \frac{4!}{2!2!}= \frac{3}{16}$
d) perdendo três e ganhando dois dos jogos de 2 a 6, e ganhando o jogo 7. Um exemplo em que isso acontece é:
| Jogo | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Vencedor | A | A | A | A | A | A | A |
| Probabilidade | 1 | $\frac{1}{2}$ | $\frac{1}{2}$ | $\frac{1}{2}$ | $\frac{1}{2}$ | $\frac{1}{2}$ | $\frac{1}{2}$ |
Considerando que os resultados dos jogos 2 a 6 podem ocorrer em qualquer ordem, o número de maneiras como esse cenário pode ocorrer é o número de permutações de BBBAA, ou $\frac{5!}{2!3!}$.
Esse cenário acontece com probabilidade: $1 \cdot \frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{2} \cdot \frac{5!}{2!3!}= \frac{5}{32}$
Portanto, o time que venceu a primeira partida é campeão com probabilidade:
$\frac{1}{8}+\frac{3}{16}+\frac{3}{16}+ \frac{5}{32}= \frac{42}{64}$
Letra C