Fique com as questões da UEMA separadas por assunto. Em cada questão temos a resposta comentada. Abaixo temos as questões da Uema sobre Geometria Espacial.
Questão 1
Q158M (UEMA) Dentre as várias aplicações do Teorema de Arquimedes, podemos utilizá-lo para calcular o volume de sólidos geométricos irregulares. Donde, podemos concluir que Vliq.desl.= Vreal do corpo, ou seja, o corpo que estiver totalmente submerso a um líquido terá o seu volume real igualado ao volume do líquido deslocado ocasionado pela imersão deste corpo. Baseado nesta afirmação, para calcularmos o volume de qualquer corpo regular ou irregular, é suficiente calcularmos o volume do líquido que foi deslocado dentro do recipiente. Obviamente, o líquido do recipiente não pode ter transbordado e o corpo deve estar totalmente submerso para que a igualdade ocorra.
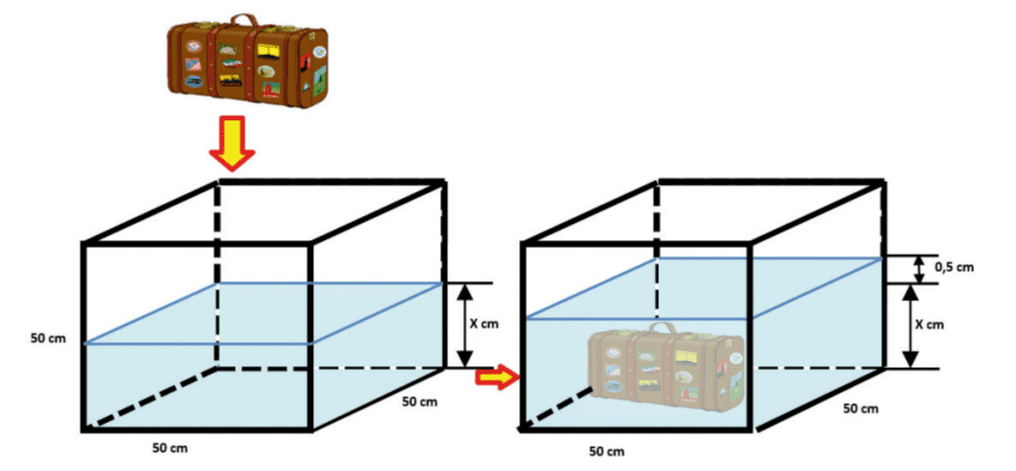
Analisando a figura e, com as informações depreendidas do texto, o volume do sólido representado é igual a:
a) 125.000 cm³
b) 123.750 cm³
c) 2.500 cm³
d) 1.250 cm³
e) 62.500 cm³
Resposta
O volume inicial é indicado por V = 50.50.x = 2500x
Acrescentando a mala (M), teremos:
$V + M = 50.50.(x + 0,5)$
$2500x + M = 2500x + 1250$
M = 1250
Letra D
Questão 2
Q163M (UEMA) Uma Agroindústria embala latas de azeitonas em conserva em caixas de papelão no formato de um paralelepípedo reto-retângulo de arestas 30 cm, 20 cm e 20 cm, respectivamente. Em cada caixa são acondicionadas 12 latas e essas caixas são dispostas, sem deixar espaço, em caixotes de madeira de 60 cm de largura por 120 cm de comprimento e 60 cm de altura. O número de latas de azeitonas em cada caixote de madeira, completamente cheio, é:
a) 540
b) 432
c) 216
d) 728
e) 864
Resposta
As caixas de papelão possuem um volume de 30.20.20 = 12000 cm³.
Já por sua vez, os caixotes de madeira que receberão as caixas, possuem um volume de
60.120.60 = 432000 cm³
Dividindo o volume total dos caixotes pelo volume correspondente a uma caixa de papelão, teremos o número de caixas de papelão que cabem no caixote de madeira. Assim,
432000/12000 = 36.
Cada caixa de papelão possui 12 latas, então 12.36 = 432 latas
Letra B
Questão 3
Q165M (UEMA) Um contêiner marítimo, usado para armazenamento, tem formato de um sólido geométrico. Os sólidos geométricos são compostos por três elementos: faces, arestas e vértices. As faces são constituídas por secções de planos; as arestas são os segmentos de retas entre as faces; os vértices estão nas extremidades das arestas. Um tubo deverá ser transportado neste contêiner. O mesmo será colocado diagonalmente no contêiner, partindo do vértice superior A ao vértice inferior B, conforme mostra a figura a seguir.

Nessas condições:
a) determine a expressão algébrica para calcular a diagonal do sólido.
b) usando as dimensões dadas na figura, calcule o comprimento máximo que um tubo pode ter, para que seja armazenado na diagonal do contêiner, desprezando o diâmetro do tubo, e que esse possa ser transportado com contêiner fechado.
Resposta
a) De modo geral, podemos encontrar o desenvolvimento de expressão algébrica que satisfaça a situação, ilustrando o paralelepípedo, teremos:
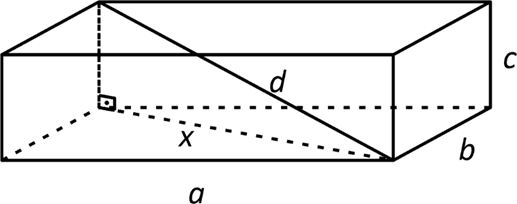
Usando a diagonal x na base do prisma e a diagonal que liga o vértice da base superior com o vértice oposto da base inferior:
Usando a diagonal x na base do prisma e a diagonal que liga o vértice da base superior com o vértice oposto da base inferior:
$\left\{ \begin{array}{cl} x^{2}= b^{2}+a^{2}\\ d^{2}=x^{2}+c^{2}\\ \end{array} \right.$
Somando as duas equações, teremos:
$x^{2} + d^{2} = b^{2} + a^{2} + x^{2} + c^{2}$
$d^{2}=b^{2}+a^{2}+c^{2} \rightarrow d=\sqrt[]{a^{2}+b^{2}+c^{2}}$
b) $T=\sqrt[]{(2,1)^{2}+(5,3)^{2}+(2,2)^{2}}$
$\sqrt[]{4,41+28,09+4,84}=\sqrt{37,34}≅6$
Questão 4
Q168M (UEMA) Qualquer quantidade de água exposta sofrerá a evaporação, pois este é um processo natural físico. Com uma piscina não seria diferente: incidência constante de sol, de calor, de vento e de baixa umidade contribui para o nível da água abaixar diariamente. Entretanto, por experiências, se diz que há um limite máximo de aproximadamente 5 cm / semana ou 3 mm / dia de evaporação, que, obviamente, varia de acordo com o tamanho da superfície da piscina e de fatores meteorológicos, como os citados acima. Provavelmente, quando esses valores são ultrapassados, a piscina apresenta problemas de vazamento.
Tendo como foco uma piscina semiolímpica, de base retangular, com 25 m de comprimento, 20 m de largura e uma profundidade uniforme de 1,3 m (da lâmina d’água até o fundo da piscina), pergunta-se:
a) Considerando o limite de 5 cm por semana de evaporação, calcule a quantidade de litros de água que restará na piscina, após uma semana sem reposição alguma de água.
b) Considerando a evaporação de 3 mm por dia, calcule quantos litros de água deverão ser recolocados na piscina, após 12 dias, para que a piscina retorne ao nível de água inicial.
Resposta
a) Volume da Piscina:
V = 25.20.1,3 = 650m³ = 650000 dm³ = 650000 L
A evaporação corresponde: E = 25.20.0,05 = 25m³.
1m³ = 1000L
25m³ = 25000 L
Restam na piscina: 650000 – 25000 = 625000
b) A evaporação corresponde: 25.20.12.0,003 = 18m³ = 18000 dm³ = 18000
Questão 5
Q174M (UEMA) O índice pluviométrico é utilizado para medir a quantidade de chuva, em milímetros, em determinado período de tempo. Seu cálculo é feito de acordo com o nível da água da chuva acumulada em um tanque aberto, em formato de um cubo, tendo uma base com 1 metro quadrado de área. Se o índice for de 30 milímetros, significa que a altura do nível de água acumulada nesse tanque mede 30 milímetros.
Um forte temporal estava prestes a acontecer. Marcos, desejando medir o índice pluviométrico, colocou uma lata, sem tampa, em formato cilíndrico de raio 300 milímetros no jardim de sua casa. Ao final da chuva, ele verificou que a altura da água, dentro da lata, era de 50 milímetros.
Calcule o índice pluviométrico encontrado por Marcos nesse temporal. Utilize 3,14 como aproximação de π.
Resposta
Ilustrando a situação:
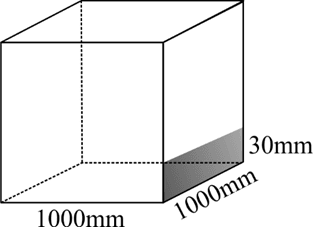
Vemos que o índice pluviométrico de 1mm é dado por 1000mm.1000mm.1mm = 1 000 000 mm³.
Na lata de Marcos, teremos:
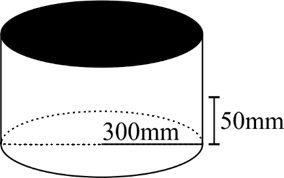
$V=π \cdot r^{2} \cdot 50 $
$ 3,14 \cdot 300^{2} \cdot 50= 14130000mm^{3}$
25m³ = 25000 L
Portanto, 14 130 000 mm³ na lata de Marcos correspondem ao índice pluviométrico de:
$\frac{{14130000}}{1000000}=14,13mm$
Questão 6
Q176M (UEMA) Observe na figura, a frente e o verso da medalha de prata das Olimpíadas do Rio.

Sua confecção é de responsabilidade do país sede do evento, obedecendo às normas do Comitê Olímpico Internacional. As dimensões mínimas das medalhas são 6 cm de diâmetro e 3 mm de espessura. As medalhas do Rio são as mais pesadas da história das Olimpíadas, com 500g. No caso específico da medalha de prata, ela é inteiramente composta por esse metal.
Assumindo que essa medalha tenha sido fabricada com diâmetro mínimo exigido, calcule a sua espessura, em centímetros.
Considere a medalha como um cilindro e que a densidade da prata é de 10,5 g/cm³. Use π = 3,14.
a) 1,588
b) 1,685
c) 1,885
d) 1,322
e) 1,191
Resposta
Ilustrando a medalha e lembrando a medalha possui 500 g de pura prata e que a densidade é 10,5 g/cm³:
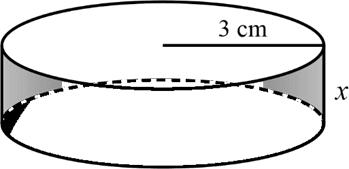
$V=π.3^{2}.x=\frac{{500}}{10,5} \rightarrow 9.3,14≅47,62$
$28,26x≅47,62≅ \rightarrow x≅1,685$
Letra B
Questão 7
Q177M (UEMA) Uma empresa de construção civil deseja construir uma caixa d’água, de forma cilíndrica, de modo que suas paredes sejam delineadas por dois círculos concêntricos de raios R= 3,5m e r = 3m, respectivamente, conforme ilustra o desenho.
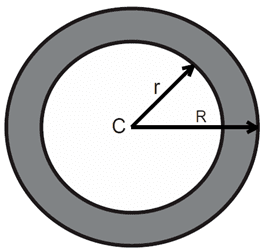
Se esse reservatório tiver altura interna igual a 8 m, o volume de concreto necessário para fazer suas paredes, no espaço compreendido entre o piso e sua parte superior, usando o valor de π = 3,14 é
a) 81,64 m³.
b) 98,00 m³.
c) 72,00 m³.
d) 153,86 m³.
e) 127,16 m³
Resposta
O volume será:
$V=h.π(R^{2}.r^{2})=8.3,14.[(3,5)^{2} – 3^{2}]$
$\downarrow$
$25,12.(3,5+3)(3,5-3)$
$\downarrow$
$25,12.6,5.0,5=81,64$
Letra A

Para mais questões por assunto clique aqui
Questão 8
Q182M (UEMA) A bola de futebol evoluiu ao longo do tempo e, atualmente, é um icosaedro truncado formado por 32 peças, denominadas de gomos e, geometricamente, de faces. Nessa bola, 12 faces são pentágonos regulares, e as outras, hexágonos, também regulares. Os lados dos pentágonos e dos hexágonos são iguais e costurados. Ao unirem-se os dois lados costurados das faces, formam-se as arestas. O encontro das arestas forma os vértices. Quando cheio, o poliedro é similar a uma esfera.

O número de arestas e o número de vértices existentes nessa bola de futebol são, respectivamente,
Pode ser utilizado o Teorema de Descartes-Euler,
A + 2 = V + F
a) 80 e 60
b) 80 e 50
c) 70 e 40
d) 90 e 60
e) 90 e 50
Resposta
No total de 32 peças, 12 são pentágonos, então 20 são hexágonos.
Vamos calcular então o total de arestas:
12.5+20.6 = 180 arestas
Cada aresta está em contato com duas peças, vamos então dividir pela metade:
180/2 = 90 arestas.
Agora vamos determinar quantos vértices possui através do teorema:
V + F = A + 2
V + 32 = 90 + 2
V = 92 – 32
V = 60 vértices
Letra D
Questão 9
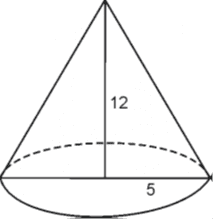
Q192M (UEMA) Um abajur tem a forma de um cone circular reto, de altura igual a 12 cm e base com raio de 5 cm. Esse abajur deverá ser revestido com um tecido que custa R\$ 0,10 o centímetro quadrado. Qual o valor gasto na aquisição do tecido necessário para o revestimento do abajur? (utilize $π = 3,14$ e $A_{l}=πrg$ ).
a) R$ 10,75
b) R$ 2,01
c) R$ 20,31
d) R$ 30,15
e) R$ 15,16
Resposta
Sendo g a geratriz do cone:
$g^{2} = 5^{2} + 12^{2} \rightarrow g=\sqrt[]{169} \rightarrow g=13$
A área total será:
$A_{l}=πrg \rightarrow A_{l}=3,14.5.13 = 204,1$
Quantidade de tecido será: T = 20,4,1.0,10 = 20,41
Questão nula
Questão 10
Q739M (UEMA) Um monumento é uma estrutura construída para homenagear um personagem ou retomar um acontecimento histórico e embelezar a arquitetura de uma cidade. Em São Luís, esta herança cultural está presente em diversas construções, como as fontes do Ribeirão e das Pedras, as ruínas do Sítio do Físico e as antigas fábricas Cânhamo e Santa Amélia. Na região do Cais da Sagração, próximo ao Palácio dos Leões, uma edificação se destaca das demais. Localizada em um enclave na Avenida Senador Vitorino Freire, a Pedra da Memória é um obelisco construído em cantaria no ano de 1841, para homenagear a maioridade (e posterior sagração) do Imperador Dom Pedro II, ocorrida em 18 de julho daquele ano. O obelisco é feito em pedra de cantaria e recebe o nome de Baluarte de São Cosme e Damião. Suas estruturas estão protegidas por muralhas que pertenciam ao antigo Forte São Felipe, onde ficava rodeado por dois canhões que já não estão mais lá.

A parte superior desse obelisco se assemelha a uma pirâmide regular quadrangular, conforme representada na figura abaixo.
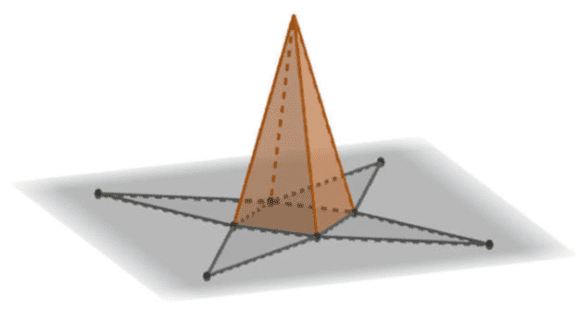
O perímetro da base e o apótema dessa pirâmide medem, respectivamente, 8,0 metros e 2,60 metros. Para aquisição do material a ser confeccionado, a informação sobre o volume é fundamental. O volume dessa pirâmide, em metros cúbicos, é igual a
a) 2,20
b) 4,80
c) 3,20
d) 4,50
e) 3,60
Resposta
Tendo o perímetro igual a 8 m, o lado da base quadrangular será igual a 8 ÷ 4 = 2 m. O apótema da base da pirâmide é metade do lado da base 2 ÷ 2 = 1
Ilustrando a situação, vamos encontrar a altura da pirâmide:
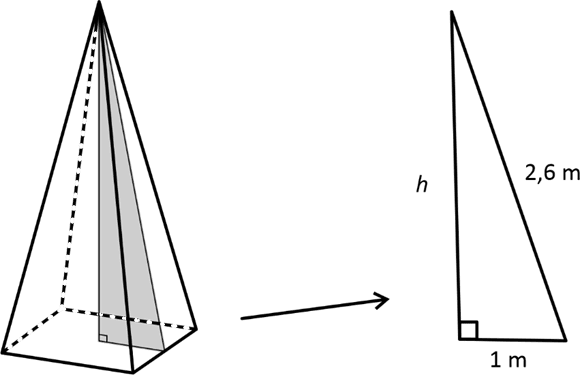
h² + 1² = 2,6 ² ⟹ h = 2,4
Agora, o volume:
$\frac{{1}}{3} \cdot 2^{2} \cdot 2,4 = \frac{{1}}{3} \cdot 9,6=3,2m^{3}$
Letra C
Questão 11
Q196M (UEMA) Um reservatório tem a forma de um cone circular reto de altura igual a 10m e raio igual a 4m (figura abaixo). Este reservatório recebe água até a altura de 5m. O volume de água presente no reservatório corresponde a:
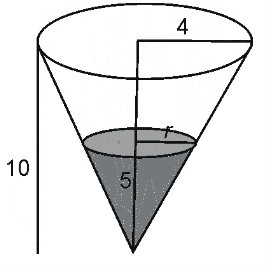
a) $\frac{{1}}{6}$ do volume total do reservatório
b) $\frac{{1}}{2}$ do volume total do reservatório
c) $\frac{{1}}{3}$ do volume total do reservatório
d) $\frac{{1}}{4}$ do volume total do reservatório
e) $\frac{{1}}{8}$ do volume total do reservatório
Resposta
Usando a semelhança de sólidos, vamos encontrar a proporção linear sendo h a altura da água e H a altura do reservatório:
$k=\frac{{h}}{H}=\frac{{5}}{10}=\frac{{1}}{2}$
Aplicando ao volume, sendo V o volume do reservatório e v o volume da água:
$k^{3}=\frac{{v}}{V} \rightarrow (\frac{{1}}{2})^{3}=\frac{{v}}{V}$
$\frac{{1}}{8}=\frac{{v}}{V} \rightarrow v=\frac{{1}}{8}V$
Letra E
Questão 12
Q212M (UEMA) Um clube de futebol, para agradar a sua torcida e a seus jogadores, resolveu homenagear os jogadores que mais se destacaram no clube na última temporada. Para isso, confeccionaram-se dezesseis troféus do mesmo tamanho, em formato de bola de futebol, com raio igual a 6. Determine (use π = 3,14)
a) a área total das superfícies consideradas.
b) o volume total dos troféus.
Resposta
a)
$A = 16.4.π.r² = 16.4.3,14.6²$
$16.12,56.36 = 7234,56 u.a$
b)
$V= \frac{{4πr^{3}}}{3} \rightarrow 16.\frac{{4π6^{3}}}{3}=\frac{{16.4.3,14.216}}{3}$
$64.3,14.72=14469,12 u.v$
Questão 13
Q578M (UEMA) O fabricante de uma das melhores bolas de basquete do país está colocando à venda uma embalagem cúbica, contendo 8 unidades, conforme a figura a seguir.
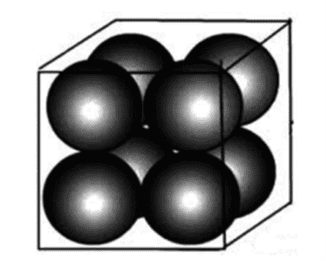
Considerando que cada bola de basquete tem raio igual a “r” cm e que tangenciam todos os lados internos das faces da embalagem cúbica, o valor, em cm³, do espaço vazio dentro da caixa, ou seja, o espaço não preenchido pelas bolas de basquete é:
a) $\frac{{32r^{3}(6-π}}{3}$
b) $\frac{{4r^{3}(48-π)}}{3}$
c) $\frac{{8r^{3}(3-4π)}}{3}$
d) $\frac{{4r^{3}(6-π)}}{3}$
e) $\frac{{32r^{3}(3-π)}}{3}$
Resposta
Para calcularmos o volume da esfera usaremos $\frac{{4}}{3}πr^{3}$ , sendo o raio da esfera r, a aresta do cubo vale 4r. O espaço vazio será:
$(4r)^{3} – 8 \cdot \frac{4}{3} \cdot πr^{3} = 64πr^{3} -\frac{32}{3} \cdot πr^{3} $
$\frac{{192r^{3}}-{32πr^{3}}}{3}=\frac{{32πr^{3}(6-π)}}{3}$
Letra A
Questão 14
Q204M (UEMA) Uma pirâmide regular de base hexagonal tem altura igual a 5 m e é interceptada por um plano paralelo a sua base a uma distância de 2 m de seu vértice, formando uma região de área igual a 25 m². A área da base dessa pirâmide é:
a) 156,25 m²
b) 165,52 m²
c) 150,00 m²
d) 125,00 m²
e) 225,00 m²
Resposta
Considerando a região de área 25m² a pirâmide semelhante seccionada, a razão linear de semelhança será:
$k=\frac{{h}}{H}=\frac{{2}}{5}$
Sendo a pirâmide maior M e a menor m, teremos:
$k^{2}=\frac{{A_{m}}}{A_{M}} \rightarrow (\frac{{2}}{5})^{2}=\frac{{25}}{A_{M}}$
$A_{M}=\frac{{625}}{4}=156,25$
Letra A
Questão 15
Q211M (UEMA) O Complexo Deodoro, que engloba as praças Deodoro, Pantheon e as alamedas Gomes de Castro e Silva Maia, no Centro de São Luís, passou por uma grande reforma. Foram colocadas esferas como objeto de decoração, conforme imagem a seguir.

Em matemática, chamamos de esfera de centro O e raio R o conjunto de pontos do espaço cuja distância ao centro é menor ou igual ao raio R e ainda que seu volume é calculado como sendo quatro terços do valor de π multiplicado pelo cubo do raio da esfera. (use π=3,14).
O raio de uma das esferas é de, aproximadamente, 20cm e todas as esferas são iguais. O volume, em centímetros cúbicos, correspondente a 10 dessas esferas, é igual a, aproximadamente:
a) 33.933,34
b) 16.746,67
c) 334.933,33
d) 188.400,00
e) 18.840,00
Resposta
Para calcularmos o volume da esfera usaremos $\frac{{4}}{3}πr^{3}$ . Como são 10 esferas, teremos:
$10.\frac{{4}}{3}.3,14.20^{3}=\frac{{40.3,14.8000}}{3}$
$\frac{{1004800}}{3}≅334933,33$
Letra C
Questão 16
Q180M (UEMA) O desenho indicado a seguir representa a planificação de um monumento situado à entrada de uma cidade com a forma de um prisma de base pentagonal regular e faces retangulares.
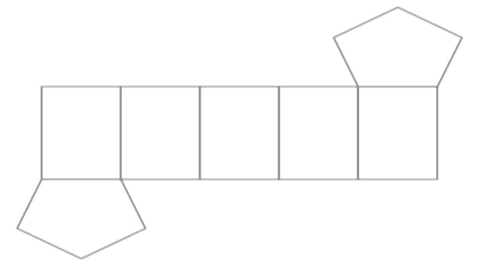
Os retângulos medem 5m por 3,6m e os pentágonos têm os lados iguais a 3,6m. Atenda aos itens indicados a seguir:
a) ilustre graficamente esse monumento;
b) calcule a quantidade necessária de material (lajotas), em m², para o revestimento das faces laterais e da base superior desse monumento. Use: tg36° = 0,72
Resposta
a)
A ilustração do sólido é a seguinte:

b)
As faces laterais são 5 retângulos de 5m por 3,6 m. A área, então:
5.5.3,6 = 90 m²
Para o cálculo da área do pentágono, precisamos do o apótema a.
Calculando o ângulo x dos triângulos, temos $5x = 360 \rightarrow x = 72°$

Assim, o apótema será dado por: $tg36°=\frac{{1,8}}{a} \rightarrow 0,72a=1,8 $
$ a=2,5m$
Agora, fazendo a área dos 5 triângulos, teremos: $5.\frac{{3,6.2,5}}{2}=5.\frac{{9}}{2}=\frac{{45}}{2}=22,5m^{2}$
Por fim, a área das faces laterais e da base superior será 90 + 22,5 = 112,5m²
Letra A
Questão 17
Q186M (UEMA) Os copos de refrigerante de uma determinada cadeia de fastfood têm capacidades de 300, 500 e 700mL, respectivamente. Esses são confeccionados em material plástico no formato de tronco de cone. Supondo que todos os copos tenham as mesmas dimensões de base, quais seriam as relações entre as suas alturas?
Resposta
Usando a fórmula do tronco de cone $V=\frac{{π.h}}{3}.(R^{2}+Rr+r^{2})$ e como todos os copos possuem a mesma dimensão de bases, consideraremos $R^{2}+Rr+r^{2}$ como uma constante k.
Para o copo de 300 mL: $300=\frac{{π.h_{1}}}{3}.k \rightarrow 900=π.h_{1}.k$
$h_{1}=\frac{{900}}{πk}$
Para o copo de 500 mL: $500=\frac{{π.h_{2}}}{3}.k \rightarrow 1500=π.h_{2}.k $
$ h_{2}=\frac{{1500}}{πk}$
Para o copo de 700 mL: $700=\frac{{π.h_{3}}}{3}.k \rightarrow 2100=π.h_{3}.k $
$ h_{3}=\frac{{2100}}{πk}$
Relacionado as alturas, teremos:
$\frac{h_{1}}{h_{2}}=\frac{\frac{900}{πk}}{\frac{1500}{πk}}=\frac{{900}}{1500}=\frac{{3}}{5}$
$\frac{h_{1}}{h_{2}}=\frac{\frac{900}{πk}}{\frac{2100}{πk}}=\frac{{900}}{2100}=\frac{{3}}{7}$
$\frac{h_{1}}{h_{2}}=\frac{\frac{1500}{πk}}{\frac{2100}{πk}}=\frac{{1500}}{2100}=\frac{{5}}{7}$
Questão 18
Q205M (UEMA) Uma pirâmide hexagonal regular de altura 12 cm e aresta da base igual a 4 cm é seccionada por um plano paralelo à base e distante 6 cm do vértice, obtendo-se um tronco de pirâmide (T1) e uma pirâmide (P1). A razão entre o volume de T1 e o volume de P1 é
a) 8
b) 7
c) 7/8
d) 2/3
e) 1/7
Resposta
Ilustrando a pirâmide (P), a pirâmide (P1) e o tronco de pirâmide (T1), nessa ordem:
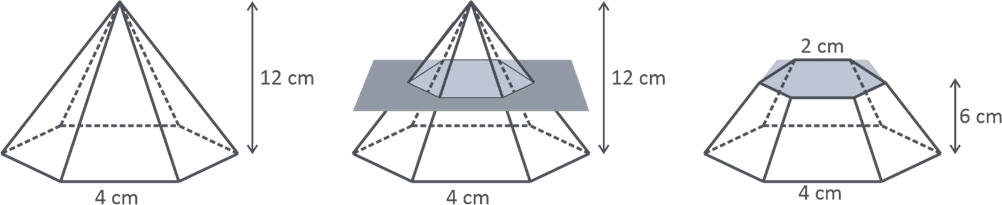
Note que $V_{T1}=V_{P}-V_{P1}$ e guarde essa informação.
Agora, usaremos a razão de semelhança entre a alturas das duas pirâmides P1 e P:
$k=\frac{{h_{P1}}}{h_{P}}=\frac{{6}}{12}=\frac{{1}}{2}$
A razão de semelhança entre os volumes das duas pirâmides P1 e P:
$k^{3}=\frac{V_{P1}}{V_{P}} \rightarrow (\frac{1}{2})^{3}==\frac{V_{P1}}{V_{P}}$
$\frac{1}{8}=\frac{V_{P1}}{V_{P}} \rightarrow V_{P}=8V_{P1}$
Retomando a equação $V_{T1}=V_{P}-V_{P1}$ , temos: $V_{T1}=8V_{P1}-V_{P1} \rightarrow V_{T1}=7V_{P1}$
A razão entre o volume de T1 e o volume de P1 é: $\frac{{V_{T1}}}{V_{P1}}=\frac{{7V_{P1}}}{V_{P1}}=7$
Letra B
