Fique com as questões da UEMA separadas por assunto. Em cada questão temos a resposta comentada. Abaixo temos as questões da Uema sobre Analise Combinatória.
Questão 01
Q228M (UEMA) O novo sistema de placas de veículos utiliza 7 caracteres, sendo um grupo de 3 letras, dentre as 26 letras do alfabeto, seguido de 4 algarismos. O DETRAN/MA, objetivando as comemorações dos 400 anos de São Luís/MA, reservou, para emplacamentos em 2012, a sequência de placas constituídas somente pelo grupo de letras S, L e Z, nessa ordem, seguida dos 4 algarismos, conforme legislação vigente. Exemplos: SLZ–0001, SLZ–0400, SLZ–7839 etc. Nessas condições, o número de placas desse tipo que poderão ser construídas para homenagear os 400 anos da capital maranhense é igual a:
a) 999
b) 1.000
c) 9.999
d) 10.000
e) 99.999
Resposta
Organizando as possibilidades em uma tabela, teremos:
| Possibilidades | LETRAS | NÚMEROS | |||||
| S | L | Z | _____ | _____ | _____ | _____ | |
| 1 | 1 | 1 | 10 | 10 | 10 | 10 | |
Ao total, temos: $10^{4}-1=10000-1=9999$
Lembre-se que não existe a placa SLZ-0000, já que a contagem parte de SLZ-0001.
Letra C
Questão 2
Q740M (UEMA) A placa Mercosul foi adotada em todo o território brasileiro, em 2020, em substituição ao modelo cinza.
Conforme o Denatran (Departamento Nacional de Trânsito), todos os carros emplacados atualmente no país utilizam o novo padrão. Criado em 2014, o padrão Mercosul é utilizado desde 2018, no Brasil. O formato também é adotado na Argentina, no Paraguai e no Uruguai, com algumas diferenças em relação à versão brasileira. A placa Mercosul é formada por três letras, um número, outra letra e dois algarismos, nessa ordem, conforme a figura abaixo.

Calcule a quantidade exata de placas, considerando as seguintes condições: Placas possíveis de serem fabricadas, de acordo com o modelo Mercosul, conforme exemplificado na figura e, considerando o alfabeto brasileiro. Essas placas devem ser iniciadas por vogal, cuja terminação seja com o algarismo 9. A quantidade de placas será de:
a) 6.083.500.
b) 8.788.000.
c) 79.092.000.
d) 44.348.715.
e) 175.760.000.
Resposta
Organizando as possibilidades em uma tabela, teremos:
| Letra | Letra | Letra | N° | Letra | N° | N° | |
| 9 | |||||||
| Possibilidades | 5 | 26 | 26 | 10 | 26 | 10 | 1 |
$5.26.26.10.26.10.1 = 8 788 000$
Letra B
Questão 3
Q262M (UEMA) Usando os números 1, 3, 4, 6 e 9, quantos números de três algarismos distintos pode-se formar?
a) 60
b) 50
c) 70
d) 40
e) 30
Resposta
$A_{5,3}= \frac{5!}{(5-3)!}= \frac{5!}{2!}= \frac{5.4.3.2!}{2!}=60$
Letra A
Questão 4
Q263M (UEMA) Um engenheiro construiu três casas de mesmo modelo e tamanho, uma junto da outra. Para pintura dessas casas, contratou um profissional que poderia escolher, a seu critério, tintas de cinco cores distintas.
Determine de quantas formas o pintor poderia escolher as tintas, de modo que as casas fossem pintadas de cores diferentes.
Resposta
$A_{5,3}= \frac{5!}{(5-3)!}= \frac{5!}{2!}= \frac{5.4.3.2!}{2!}=60$
Letra A
Questão 5
Q279M (UEMA) Anagramas, no âmbito da matemática, estão relacionados com a análise combinatória e consistem na permutação (troca de posição das letras) de uma palavra, resultando outra formação com exatamente as mesmas letras, podendo ter significado presente no dicionário ou não. Para sabermos o total de anagramas que são possíveis de serem formados, usamos o conceito de fatorial.
Por exemplo a palavra ALEGRIA com 7 letras, o resultado é 7! (7x6x5x4x3x2x1 = 5040) e para obter os anagramas basta trocar as letras entre si.
A quantidade de anagramas formados com a palavra PEDRA e quatro exemplos adequados destes anagramas estão indicados na seguinte opção:
| Quantidade de Anagramas | Exemplos de Anagramas | |
| a) | 120 | PERDA – DRAEP – DEPRA – DRAPE |
| b) | 60 | PARDE – DREPA – PERDI – DIPRA |
| c) | 60 | ERDAP – ORDEP – PADRE – DAPRA |
| d) | 240 | PERDE – ADREP – PRAED – ARPED |
| e) | 120 | PERDA – EPDRA – MADRE – ADPRA |
Resposta
Como a palavra PEDRA possui 5 letras diferentes, faremos:
$P_{5}=5!=120$
Note que na letra E temos um anagrama (MADRE) que não pertence ao conjunto de anagramas da palavra PEDRA.
Letra A

Para mais questões por assunto clique aqui
Questão 6
Q281M (UEMA) Três casais vão ao cinema e observam que existem 6 poltronas livres em uma determinada fileira. De quantas maneiras diferentes os casais podem ocupar essas poltronas, de modo que cada casal fique sempre junto?
a) 24
b) 12
c) 16
d) 6
e) 32
Resposta
Temos que os casais devem estar sempre juntos, assim, vamos “amarrar” em uma única poltrona dois a dois, ficando uma permutação de 3 casais: $P_{3}=3!=3.2.1=6$. Como os casais não estão ordenados, eles permutam entre si, ou seja:
$2.2.2 = 8$. Assim, como resultado, teremos:
$6.8 = 48$, questão anulada.
Questão 7
Q295M (UEMA) Aproveitando a Semana de Promoções de um Shopping Center, um jovem verifica que tem dinheiro para comprar apenas 3 dos 24 DVDs disponíveis em uma loja. De quantas maneiras diferentes esse jovem poderá fazer sua escolha?
a) 512
b) 4048
c) 2024
d) 3036
e) 1012
Resposta
$C_{24,3}=\frac{{24!}}{3!(24-3)!}=\frac{{24.23.22.21!}}{3.2.21!}$
$\downarrow$
$8.23.11=2024$
Letra C
Questão 8
Q296M (UEMA) No regulamento do campeonato brasileiro de futebol da série C de 2018, nos artigos 11 e 12, lê–se:
Na primeira fase os 20 (vinte) clubes constituirão os grupos A e B com 10 (dez) clubes cada, dentro de cada grupo todos os clubes jogarão entre si, em turno (ida) e returno (volta).
Calcule a quantidade de jogos do turno (ida) que foram realizados no grupo A.
Resposta
$C_{10,2}=\frac{{10!}}{2!(10-2)!}=\frac{{10.9.8!}}{2!.8!}=\frac{{10.9}}{2}=45$
Questão 9
Q305M (UEMA) A rádio comunitária de Santa Teresa anunciou que o PCL estava reunido para escolher 8 candidatos a vereador da cidade pelo partido para concorrer às próximas eleições. O partido dispõe de 13 candidatos a candidatos a vereador, sendo 3 mulheres e 10 homens. Segundo o regimento interno do partido, ao menos 25% dos candidatos do PCL são obrigatoriamente mulheres. O locutor da rádio ofereceu um prêmio a quem prever a lista com os 8 escolhidos. O Sr. Lourival foi o vencedor da premiação, pois ele listou todas as possíveis composições dos 8 candidatos, respeitando o regimento interno do partido. Quantas listas o Sr. Lourival enviou à rádio indicando os possíveis candidatos?
a) 882 listas
b) 1782 listas
c) 1287 listas
d) 462 listas
e) 630 listas
Resposta
A lista possuirá 8 escolhidos dentre eles ao menos 25% são mulheres. Assim, teremos duas situações a considerar:
1ª, duas mulheres na lista (25% de 8)
2ª, 3 mulheres na lista.
Para duas mulheres na lista:
| mulheres | homens | ||||||
| _____ | _____ | _____ | _____ | _____ | _____ | _____ | _____ |
| $C_{3,2}$ | $C_{10,6}$ | ||||||
Totalizando: $C_{3,2}.C_{10,6}=\frac{{3!}}{2!1!} \cdot \frac{{10!}}{6!4!}$
$\downarrow$
$\frac{{3.2.10.9.8.7.6!}}{2.6!4.3.2}=10.9.7=630$
Para três mulheres na lista:
| mulheres | homens | ||||||
| _____ | _____ | _____ | _____ | _____ | _____ | _____ | _____ |
| $C_{3,3}$ | $C_{10,5}$ | ||||||
Totalizando: $C_{3,3}.C_{10,5}=1.\frac{{10!}}{5!5!} \cdot \frac{{10!}}{6!4!}$
$\downarrow$
$\frac{{10.9.8.7.6.5!}}{5.4.3.2.5!}=2.9.2.7=252$
Somando, temos 630 + 252 = 882
Letra A
Questão 10
Q346M (UEMA) Uma professora de educação infantil de uma escola, durante a recreação de seus 6 alunos, organiza-os em círculos para brincar. Considere a seguinte forma de organização dos alunos pela professora: são três meninas e três meninos e cada menina ficará ao lado de um menino, de modo alternado. As possibilidades de organização dos seus alunos são
a) 4.
b) 6.
c) 9.
d) 12.
e) 16.
Resposta
Para entendermos o problema, vamos considerar a figura abaixo com as meninas m1, m2 e m3; e meninos h1, h2 e h3:
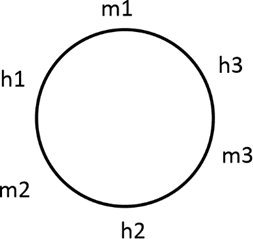
Como devem estar em casal, fixaremos as duplas (3 duplas) para permutarem de forma circular
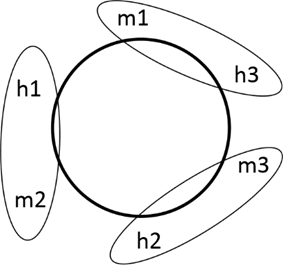
Portanto, devemos permutar de forma linear somente os meninos ou somente as meninas, já que se permutarmos os dois faremos combinações já existentes (duplas que já foram feitas). Portanto, permutando os meninos:
$P_{C}3.P_{3}=(3-1)!.3!=2.3.2.1=12$
Letra D
