Fique com as questões da UEMA separadas por assunto. Em cada questão temos a resposta comentada. Abaixo temos as questões da Uema sobre Triângulos
Questão 1
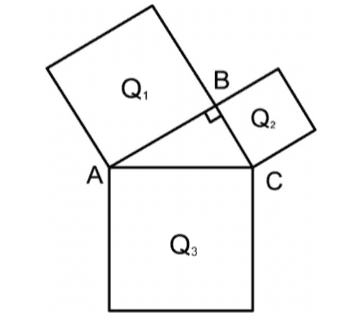
Q970F (UEMA) A figura indicada a seguir é constituída por três quadrados Q1, Q2, Q3 e um triângulo retângulo BAC
Sabendo–se que a área de Q1 vale 256 cm² e que a área de Q2 vale 144 cm², então o perímetro desse triângulo mede:
a) 36 cm
b) 52 cm
c) 48 cm
d) 24 cm
e) 60 cm
Resposta
$256 + 144 = CB^{2} \rightarrow CB = 20$
$P = 16 +12 + 20 = 48$
Letra C
Questão 2
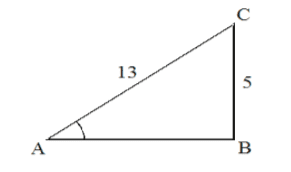
Q1001F (UEMA) Na figura abaixo, o triângulo ABC é retângulo em B. O cosseno do ângulo BÂC é:
a)$\frac{{11}}{13}$
b)$\frac{{10}}{13}$
c)$\frac{{12}}{13}$
d)$\frac{{6}}{13}$
e)$\frac{{1}}{13}$
Resposta
Descobrindo o lado AB:
$13^{2} = 5^{2} + AB^{2} \rightarrow 169 – 25 = AB^{2}$
$AB = \sqrt[]{144} \rightarrow AB = 12$
Aplicando cosseno
$cos \alpha = \frac{{12}}{13}$
Letra C
Questão 3
Q1658F (UEMA) O triângulo de sinalização, também chamado de dispositivo de sinalização luminosa e refletora de emergência, é um item obrigatório em todos os automóveis, de uso fundamental para avisar aos outros motoristas quando há alguém parado logo à frente, evitando, assim, acidentes. Esse triângulo de sinalização é previsto em lei pela resolução do CONTRAN nº 014/98 e suas especificações técnicas constam na resolução nº 827/96. Trata-se de um triângulo equilátero vermelho, com dimensão de 50cm de lado e 5cm de espessura na parte vermelha, conforme resolução nº 37/01 do MERCOSUL, que estabelece o padrão de triângulo de segurança, conforme o modelo. Para construí-lo, é necessário conhecer a medida de sua área para aquisição de material específico.

Consideremos que o referido triângulo fosse confeccionado completamente com o material vermelho, ou seja, sem orifício interno.
Nessas condições, a área total do triângulo, considerando, apenas, a medida do lado, corresponde, em cm², a:
a) 1385,60
b) 1167,75
c) 1237,50
d) 1102,88
e) 1082,50
Resposta
O problema nos traz um triângulo equilátero com lado igual a 50 cm. Pela fórmula:
$A=\frac{{L^{2} \sqrt[]{3}}}{4}=\frac{{50^{2} \sqrt[]{3}}}{4}=625\sqrt[]{3}$
$≅ 625 \cdot 1,73 ≅ 1081,25$
Aplicando cosseno
Letra B
Questão 4
Q1068F (UEMA) Gabrielle e sua família mudaram-se para uma casa nova. Ao saber que teria seu próprio quarto, Gabrielle tratou de decorar, com papel de parede, o lado em que fica a janela. Pesquisou, na planta, as dimensões do quarto e observou que essa parede possui 2,50m x 2,80m
Sabendo-se que a janela mede 1m x 1,20m, a quantidade de papel de parede, em metros quadrados, a ser utilizada para a decoração é de:
a) 5,5
b) 5,8
c) 6,3
d) 7,0
e) 8,2
Resposta
A área da parede será 2,5m.2,8m = 7m²
A área da janela será 1m.1,2m = 1,2m²
A quantidade de papel de parede será: 7m²-1,2m²= 5,8 m²
Letra B
Questão 5
Q1058F (UEMA) O pátio de uma escola tem a forma triangular em que dois dos seus lados medem 50 m e 60 m, respectivamente. Sabendo–se que esses dois lados formam entre si um ângulo de 60°,determine a área desse pátio. (Use:$\sqrt[]{3}= 1,7$).
Resposta
Usando a fórmula da área de um triângulo: $A=\frac{{1}}{2} \cdot a \cdot b \cdot sen\alpha$
$\frac{{1}}{2}.50.60.sen60=25.60.\frac{{\sqrt[]{3}}}{2}$
$\downarrow$
$30.25.1,7=1275$
Questão 6
Q947F (UEMA) Nos últimos anos, tornou–se evidente que os cabos ópticos estão substituindo o fio de cobre como um meio apropriado de transmissão do sinal de comunicação. O funcionamento das fibras ópticas é semelhante ao sistema de fios de cobre que está sendo substituído. A diferença é que as fibras ópticas funcionam pelo Princípio da Reflexão Total que ocorre, quando os raios de luz que seguem determinados percursos dentro da fibra são totalmente refletidos na interface núcleo–casca, permanecendo no interior do núcleo.
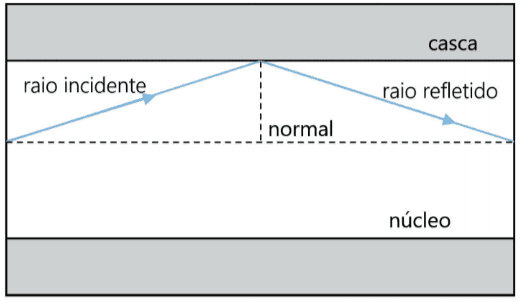
Conforme a figura, o ângulo entre o raio incidente e o raio refletido na fibra óptica é de 110°. Considere que a parede interna da fibra óptica se comporta como um espelho plano. O ângulo entre o raio refletido e a casca de fibra ótica é igual a
a) 43°
b) 45°
c) 35°
d) 55°
e) 110°
Resposta
Ilustrando asituação, teremos:
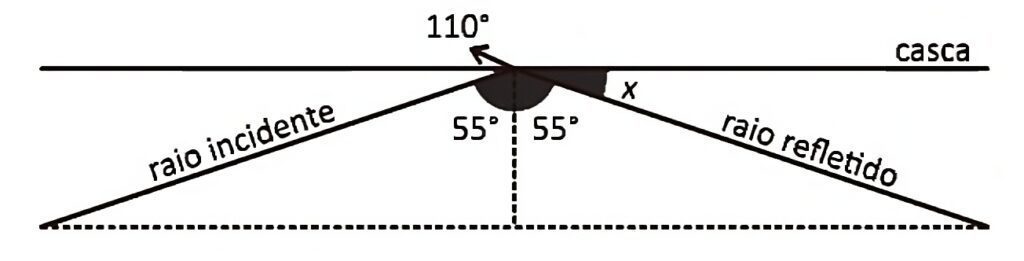
$55 + x = 90 \rightarrow x=35$
Letra C

Para mais questões por assunto clique aqui
Questão 7
Q1032F (UEMA) As cidades de Alegrete, Ruínas e Águas Lindas encontram–se interligadas por estradas que obedecem à disposição indicada no gráfico apresentado a seguir:
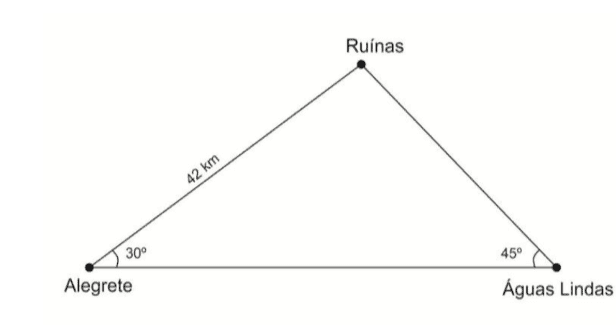
Atenda aos itens solicitados a seguir:
a) Enuncie a “lei dos senos”, que estabelece a relação entre a medida de um lado de um triângulo e o seno do ângulo oposto a esse lado;
b) Use o resultado indicado no item a, para calcular a distância aproximada entre Ruínas e Águas Lindas. Use $\sqrt[]{2}=1,414, sen30°=\frac{{1}}{2}, sen45°=\frac{{\sqrt[]{2}}}{2}$
Resposta
a)
A lei dos senos diz que os lados de um triângulo são proporcionais aos senos dosângulos opostos aestes lados e a constante de proporcionalidade é o diâmetro da circunferência circunscrita ao triângulo.
b)
Sendo d a distância pedida, faremos:
$\frac{{42}}{sen45°}=\frac{{d}}{sen30°} \rightarrow \frac{{42}}{\frac{{\sqrt[]{2}}}{2}}=\frac{{d}}{\frac{{1}}{2}}$
$42.\frac{{1}}{2}=d.\frac{{\sqrt[]{2}}}{2} \rightarrow 42=d.\sqrt[]{2}$
$d= \frac{{42}}{1,414}≅29,70$
Questão 8
Q1024F (UEMA) O Porto do Itaqui, porto brasileiro localizado na cidade de São Luís do estado do Maranhão, é nacionalmente conhecido por ter uma das maiores amplitudes de maré do Brasil, podendo ultrapassar 7 metros. O Itaqui é o 11º no ranking geral e o 6º entre os portos públicos em movimentação de cargas. A profundidade de seu canal de acesso é de 23 metros. Frequentemente, existem navios atracando, descarregando, desatracando e à espera na baía de São Marcos.
Analise a imagem a seguir.
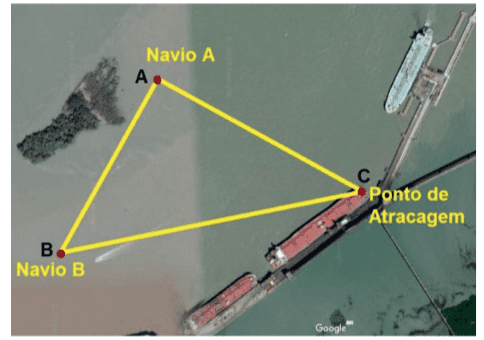
Considere a medida do ângulo ACB=60°, a distância AC igual a 5 km e a distância CB igual a 8km. Nessas condições: (Use cos 60°=0,5), calcule a distância do navio A até o navio B, em km.
Resposta
Ilustrando a situação e usando a Lei dos Cossenos em triângulos quaisquer:
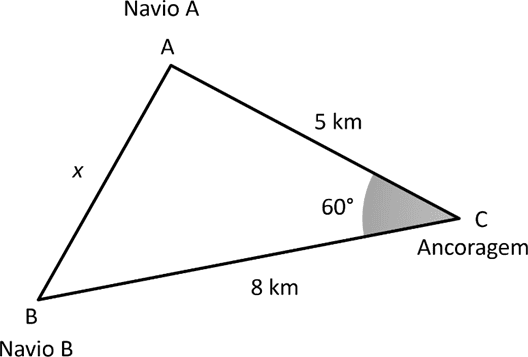
$x=5²+8²-2.5.8.cos60° $
$x²=25+64-80.0,5=49$
$x=7$
Questão 9
Q1006F (UEMA) O Centro de Lançamento de Alcântara–CLA, no Maranhão, segundo o presidente da Agência Espacial Brasileira– AEB, está preparado para lançamento de pequenos satélites, com até200kg, para órbita baixa e média–a cerca de 600 km de altitude e foguetes de até 100 toneladas no máximo. Ainda segundo o presidente da AEB, Alcântara é um dos melhores locais do mundo para lançamento de foguetes por conta da localização: próxima à linha do Equador, ela faz com que os custos sejam até 30% menores com a boa capacidade angular de órbitas
Um foguete foi lançado verticalmente para órbita e quando atingiu 8km de altura foi avistado por uma pessoa A em São Luís sob o ângulo de 45° e, no mesmo instante, e com posição alinhada com
primeira, foi avistado, também, por outra pessoa B sob o ângulo de 30°. Use $\sqrt[]{3}=1,73$ $tg30°=\frac{{\sqrt[]{3}}}{3}, tg°45=1.$

Analisando a situação apresentada, pode–se afirmar que a distância, em km, aproximada da pessoa A até a pessoa B é de:
a) 13,87
b) 5,87
c) 8,00
d) 21,87
e) 12,62
Resposta
Ilustrando a situação temos a seguinte figura:
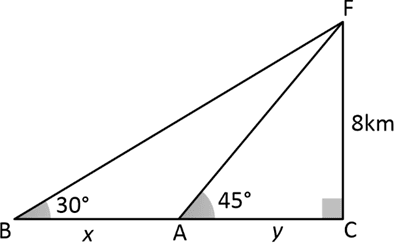
Agora, aplicando tg45° no triângulo ACF:
$tg°45=\frac{{8}}{y} \rightarrow 1=\frac{{8}}{y} \rightarrow y=8 $
Agora, aplicando tg30° no triângulo BCF, teremos:
$tg°30=\frac{{8}}{x+y} \rightarrow \frac{{\sqrt[]{3}}}{3}=\frac{{8}}{x+8}$
$\sqrt[]{3}.(x+8)=24 \rightarrow x+8=\frac{{24}}{\sqrt[]{3}}$
$x ≅ 13,87 – 8 \rightarrow x ≅ 5,87$
Letra B
Questão 10
Q1351F (UEMA) Uma peça triangular, medindo 10m, 8m e 6m, feita de chapa uniforme, será içada por um guindaste por apenas um único ponto de contato, conforme a figura a seguir.
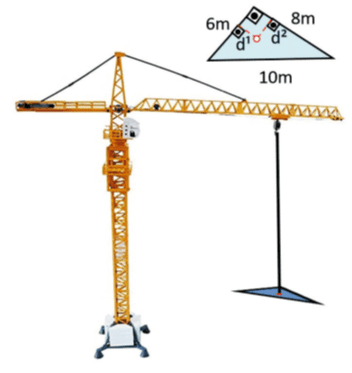
As distâncias d¹ e d², em metros, do ponto de içamento em relação aos menores lados desse triângulo para que a peça seja içada exatamente pelo ponto de encontro das três medianas são iguais a:
a) 8/3 e 2
b) 5/3 e 2/3
c) 8/45 e 16/45
d) 10/3 e 3
e) 5 e 13/3
Resposta
Ilustrando a situação e traçando as medianas pedidas, teremos:
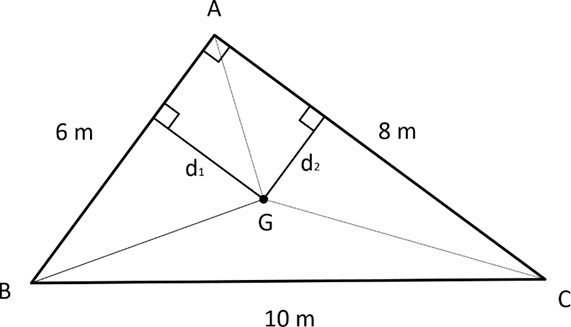
O triângulo ABC é possui área igual: $\frac{{6 \cdot 8}}{2}=24$
O ponto G é o baricentro do triângulo ABC, logo os triângulos ABG, ACG e BCG possuem mesma área. Assim:
Agora, aplicando tg30° no triângulo BCF, teremos:
$A_{ABG}=\frac{{6 \cdot d_{1}}}{2} \rightarrow \frac{{24}}{3}=\frac{{6 \cdot d_{1}}}{2}$
$\downarrow$
$8=3 \cdot d_{1} \rightarrow d_{1}=\frac{{8}}{3}$
$A_{ACG}=\frac{{8 \cdot d_{2}}}{2} \rightarrow \frac{{24}}{3}=\frac{{8 \cdot d_{2}}}{2}$
$\downarrow$
$8=4 \cdot d_{2} \rightarrow d_{2}=2$
Letra A
Questão 11
Q1035F (UEMA) A falta de rede de esgoto nas zonas rurais é um grande problema de saúde pública. Muitas propriedades rurais têm fossas rudimentares, que são, apenas, buracos para receber os dejetos. O problema dessas fossas é que elas contribuem para a contaminação do lençol freático os vírus e as bactérias presentes no material chegam aos poços que abastecem as casas e as plantações. As consequências desse ciclo são as doenças causadas por bactérias fecais, que se espalham rapidamente pela água. Em lugares onde não existe rede pública de abastecimento de água, é comum obter–se água no domicílio através de métodos paliativos tais como: poços comuns, semiartesiano, artesiano, fontes/minas, entre outras.
Deve–se respeitar por medida de segurança, a distânciamínima de 15 metros, entre o poço e qualquer tipo de fossa e de 45 metros dos demais focos de contaminação, como chiqueiros, estábulos, valões de esgotos, galeria de infiltração e outros, que possam comprometer o lençold’água que alimenta o poço.
Em uma propriedade rural, deseja–se construir uma residência (ponto A), implantar um poço artesiano (ponto B) e um local de coleta de esgoto (ponto C).
Após o reconhecimento da área, o técnico responsável pela construção optou por um modelo matemático triangular, com os seguintes dados: a distância entre B e C é 1 km, o ângulo entre os lados $\overline{AB}$ e $\overline{BC}$ é 105° e o ângulo entre os lados $\overline{AB}$ e $\overline{AC}$ é 30°.
Ilustre a situação com um desenho. A seguir, calcule a distância, em metros, da residência até o poço artesiano. Use $\sqrt[]{2} = 1,41$
Resposta
Ilustrando a situação e transformando 1km em 1000 m, teremos:
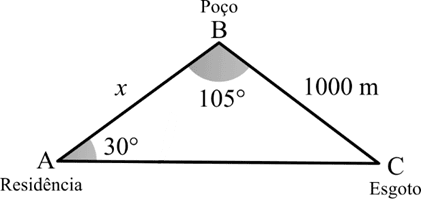
Como a soma dos ângulos internos de um triângulo é igual a 180°, temos que o ângulo = °45. Usaremos a lei dos senos:
$\frac{{sen\hat{C}}}{x}=\frac{{sen30°}}{1000} \rightarrow \frac{{sen45°}}{x} = \frac{{sen30°}}{1000}$
$\downarrow$
$\frac{\frac{\sqrt[]{2}}{2}}{x}=\frac{\frac{1}{2}}{1000}$
$\downarrow$
$\frac{\sqrt[]{2}}{2} \cdot \frac{{1}}{x}=\frac{1}{2} \cdot \frac{1}{1000}$
$\downarrow$
$\frac{\sqrt[]{2}}{2} = \frac{{1}}{2000}$
$\downarrow$
$2x=2000 \cdot \sqrt[]{2} \rightarrow x=\frac{{2000.1,41}}{2}$
$x=1410m$
Questão 12
Q1047F (UEMA) Analise a situação a seguir: Um arquiteto foi contratado para decorar a entrada de um templo religioso, no formato de um triângulo equilátero, com uma porta de madeira, cujas dimensões medem 1,05 m por 2,5 m, inserida neste triângulo. Sabe–se ainda que a altura do triângulo mede 4,25 m e que a área da porta não receberá decoração. A área, em metros quadrados, a ser decorada é igual a (Use $\sqrt[]{3} = 1,7$).
a) 10,0.
b) 9,5.
c) 8,5.
d) 8,0.
e) 7,0.
Resposta
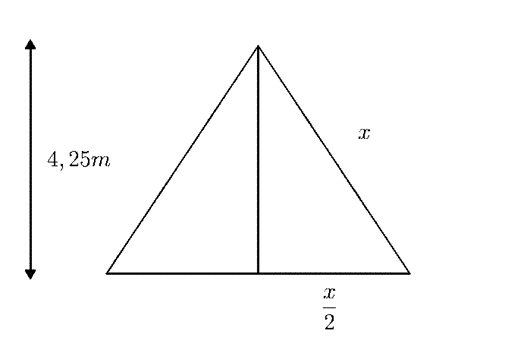
$(\frac{{x}}{2})^{2} + 4,25^{2}=x^{2} \rightarrow \frac{x^{2}}{4}+4,25^{2}=x^{2}$
$x^{2}+4.4,25^{2}=4x^{2} \rightarrow 3x^{2}=4.4,25^{2}$
$x=\sqrt[]{\frac{4.4,25^{2}}{3}} \rightarrow x=\frac{2.4,25}{\sqrt[]{3}}=\frac{{8,50}}{1,7}=5$
$A_{t}=\frac{{5.4,25}}{2}=2,5.4,25=10,625$
$A_{p}=1,05.2,5=2,625$
$A=10,25-2,625=8$
Letra D
